题目内容
4.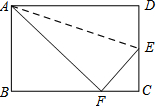 如图,折叠矩形纸片ABCD的一边AD,使点D落在BC边的点F处,已知AB=8 cm,BC=10 cm,则EC的长( )
如图,折叠矩形纸片ABCD的一边AD,使点D落在BC边的点F处,已知AB=8 cm,BC=10 cm,则EC的长( )| A. | 3 cm | B. | 4 cm | C. | 5 cm | D. | 6 cm |
分析 根据翻折的性质,先在Rt△ABF中求出BF,进而得出FC的长,然后设CE=x,EF=8-x,从而在Rt△CFE中应用勾股定理可解出x的值,即能得出CE的长度.
解答 解:由翻折的性质可得:AD=AF=BC=10cm,
在Rt△ABF中可得:BF=$\sqrt{A{F}^{2}-A{B}^{2}}$=6cm,
∴FC=BC-BF=4cm,
设CE=x,EF=DE=8-x,
则在Rt△ECF中,EF2=EC2+CF2,
即x2+16=(8-x)2,
解得:x=3,
故CE=3cm;
故选:A.
点评 本题通过折叠变换考查学生的逻辑思维能力,解决本题的关键是结合图形,首先根据翻折的性质得到一些相等的线段,然后灵活运用勾股定理进行解答.

练习册系列答案
相关题目
14.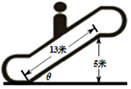 如下图,某超市的自动扶梯长度为13米,该自动扶梯到达的最大高度是5米,设自动扶梯与地面所成的角为θ,则tanθ=( )
如下图,某超市的自动扶梯长度为13米,该自动扶梯到达的最大高度是5米,设自动扶梯与地面所成的角为θ,则tanθ=( )
 如下图,某超市的自动扶梯长度为13米,该自动扶梯到达的最大高度是5米,设自动扶梯与地面所成的角为θ,则tanθ=( )
如下图,某超市的自动扶梯长度为13米,该自动扶梯到达的最大高度是5米,设自动扶梯与地面所成的角为θ,则tanθ=( )| A. | $\frac{5}{13}$ | B. | $\frac{13}{12}$ | C. | $\frac{5}{12}$ | D. | $\frac{12}{5}$ |
15. 如图,∠BAC=90°,AD⊥BC,则图中互余的角有( )
如图,∠BAC=90°,AD⊥BC,则图中互余的角有( )
 如图,∠BAC=90°,AD⊥BC,则图中互余的角有( )
如图,∠BAC=90°,AD⊥BC,则图中互余的角有( )| A. | 2对 | B. | 3对 | C. | 4对 | D. | 5对 |
12.稀土元素有独特的性能和广泛的应用,我国稀土资源的总储藏量为1050008000吨,是全世界稀土资源最丰富的国家,用科学记数法表示为( )
| A. | 1.05×1010吨 | B. | 1.05×109吨 | C. | 10.5×108吨 | D. | 1.105×1010吨 |
13.下列计算正确的是( )
| A. | xm+xm=x2m | B. | x3•x3=x6 | C. | 2-2=-4 | D. | x6÷x2=x3 |