题目内容
先观察下列等式,然后用你发现的规律解答下列问题. ,
, ,
, ,┅┅
,┅┅
(1)根据你发现的规律写出第5个等式:______.
(2)探究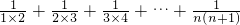 =______.(用含有n的式子表示)
=______.(用含有n的式子表示)
(3)计算: ┅┅
┅┅ .
.
解:(1) ;
;
(2)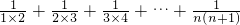
=1- +
+ -
- +
+ -
- +…+
+…+ -
-
= ;
;
(3) ┅┅
┅┅
=
=
= .
.
故答案为: .
.  .
.
分析:(1)观察发现,每一个等式的左边都是一个分数,其中分子是1,分母是连续的两个正整数之积,并且如果是第n个等式,分母中的第一个因数就是n,第二个因数是n+1;等式的右边是两个分数的差,这两个分数的分子都是1,分母是连续的两个正整数,并且是第n个等式,被减数的分母就是n,减数的分母是n+1.然后把n=5代入即可得出第5个等式;
(2)先将(1)中发现的第n个等式的规律 =
= 代入,再计算即可;
代入,再计算即可;
(3)先类比(1)的规律,得出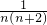 =
= (
( ),再计算即可.
),再计算即可.
点评:本题考查了规律型:数字的变化,得出 =
= ,
,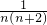 =
= (
( ),以及抵消法的运用是解题的关键.
),以及抵消法的运用是解题的关键.
 ;
;(2)
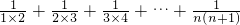
=1-
 +
+ -
- +
+ -
- +…+
+…+ -
-
=
 ;
;(3)
 ┅┅
┅┅
=

=

=
 .
.故答案为:
 .
.  .
.分析:(1)观察发现,每一个等式的左边都是一个分数,其中分子是1,分母是连续的两个正整数之积,并且如果是第n个等式,分母中的第一个因数就是n,第二个因数是n+1;等式的右边是两个分数的差,这两个分数的分子都是1,分母是连续的两个正整数,并且是第n个等式,被减数的分母就是n,减数的分母是n+1.然后把n=5代入即可得出第5个等式;
(2)先将(1)中发现的第n个等式的规律
 =
= 代入,再计算即可;
代入,再计算即可;(3)先类比(1)的规律,得出
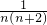 =
= (
( ),再计算即可.
),再计算即可.点评:本题考查了规律型:数字的变化,得出
 =
= ,
,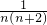 =
= (
( ),以及抵消法的运用是解题的关键.
),以及抵消法的运用是解题的关键. 
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目