题目内容
17.已知(x2-x+1)6=a0x12+a1x11+a2x10+…+a11x+a12,求a0+a2+a4+…+a12的值.分析 我们很难将(x2一x+1)6的展开式写出,因此想通过展开式去求出每一个系数是不实际的,事实上,上列等式在x的允许值范围内取任何一个值代入计算,等式都成立,考虑用赋值法解.
解答 解:令x=1,由已知等式得a12+a11+…+a2+a1+a0=1,①
令x=-1,得a12-a11+…+a2-a1+a0=729,②
①+②得2(a12+a10+a8+a6+a4+a2+a0)=730.
故a12+a10+a8+a6+a4+a2+a0=365.
点评 此题考查代数式的值,在解数学题时,将问题中的某些元素用适当的数表示,再进行运算、推理解题的方法叫赋值法,非常规数学问题通过赋值,把问题“数学化”

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
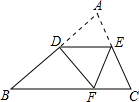 如图,D是AB边上的中点,DE∥BC,将△ABC沿过D的直线折叠,使点A落在BC上F处,
如图,D是AB边上的中点,DE∥BC,将△ABC沿过D的直线折叠,使点A落在BC上F处,