题目内容
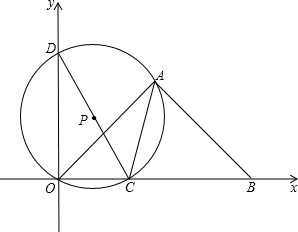 如图,等腰三角形ABO的斜边OB在x轴上,O是坐标原点,点A在第一象限内,OB=2,点C是线段OB上一动点(不与O、B重合),△OAC的外接圆P与y轴的另一交点为D,求线段CD长度的最小值.
如图,等腰三角形ABO的斜边OB在x轴上,O是坐标原点,点A在第一象限内,OB=2,点C是线段OB上一动点(不与O、B重合),△OAC的外接圆P与y轴的另一交点为D,求线段CD长度的最小值.考点:圆的综合题
专题:综合题
分析:连接PA,AC,作AH⊥OB,如图,设⊙P的半径为R,由于∠DOC=90°,根据圆周角定理得到DC为⊙P的直径,则有DC=2R,再根据等腰直角三角形的性质得到∠AOB=90°,AH=
OB=1,于是利用圆周角定理得到∠APC=2∠AOC=90°,则可判断△PAC为等腰直角三角形,所以AC=
R;由于要使CD最小,则R最小,而AC最小时,R最小,此时AC=AH=1,即R=
,于是得到线段CD长度的最小值=
.
| 1 |
| 2 |
| 2 |
| ||
| 2 |
| 2 |
解答: 解:连接PA,AC,作AH⊥OB,如图,设⊙P的半径为R,
解:连接PA,AC,作AH⊥OB,如图,设⊙P的半径为R,
∵∠DOC=90°,
∴DC为⊙P的直径,
∴DC=2R,
∵△OAB为等腰直角三角形,
∴∠AOB=90°,AH=
OB=1,
∴∠APC=2∠AOC=90°,
而PA=PC=R,
∴AC=
R,
当R最小时,CD最小,
而AC最小时,R最小,此时AC=AH=1,即
R=1,R=
,
∴线段CD长度的最小值=2×
=
.
 解:连接PA,AC,作AH⊥OB,如图,设⊙P的半径为R,
解:连接PA,AC,作AH⊥OB,如图,设⊙P的半径为R,∵∠DOC=90°,
∴DC为⊙P的直径,
∴DC=2R,
∵△OAB为等腰直角三角形,
∴∠AOB=90°,AH=
| 1 |
| 2 |
∴∠APC=2∠AOC=90°,
而PA=PC=R,
∴AC=
| 2 |
当R最小时,CD最小,
而AC最小时,R最小,此时AC=AH=1,即
| 2 |
| ||
| 2 |
∴线段CD长度的最小值=2×
| ||
| 2 |
| 2 |
点评:本题考查了圆的综合题:熟练掌握圆周角定理;会运用等腰直角三角形的性质计算角度和线段的长.

练习册系列答案
相关题目
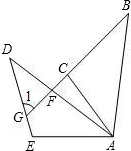 如图所示,△ABC≌△ADE,AB=AD,AC=AE,BC的延长线交DA于点F,交DE于点G,∠AED=105°,∠CAD=15°,∠B=30°,求∠1的度数.
如图所示,△ABC≌△ADE,AB=AD,AC=AE,BC的延长线交DA于点F,交DE于点G,∠AED=105°,∠CAD=15°,∠B=30°,求∠1的度数. 如图,△ABC中,AB=AC,D在BC上,且DE∥AC,DF=DC.求证:△DFC∽△ABC.
如图,△ABC中,AB=AC,D在BC上,且DE∥AC,DF=DC.求证:△DFC∽△ABC.