题目内容
如图，△ABC中，AB=AC，D在BC上，且DE∥AC，DF=DC．求证：△DFC∽△ABC．考点：相似三角形的判定
专题：证明题
分析：利用“两角法”可以证得：△DFC∽△ABC．
解答：证明：∵DE∥AC，
∴∠EDB=∠C．
∵AB=AC，
∴∠B=∠C，
∴∠EDB=∠C，
∵DF=DC，
∴∠DFC=∠C，
∴∠B=∠C=∠CFD，
∴△DFC∽△ABC．
∴∠EDB=∠C．
∵AB=AC，
∴∠B=∠C，
∴∠EDB=∠C，
∵DF=DC，
∴∠DFC=∠C，
∴∠B=∠C=∠CFD，
∴△DFC∽△ABC．
点评：本题考查了相似三角形的判定．
（1）平行线法：平行于三角形的一边的直线与其他两边相交，所构成的三角形与原三角形相似；
（2）三边法：三组对应边的比相等的两个三角形相似；
（3）两边及其夹角法：两组对应边的比相等且夹角对应相等的两个三角形相似；
（4）两角法：有两组角对应相等的两个三角形相似．
（1）平行线法：平行于三角形的一边的直线与其他两边相交，所构成的三角形与原三角形相似；
（2）三边法：三组对应边的比相等的两个三角形相似；
（3）两边及其夹角法：两组对应边的比相等且夹角对应相等的两个三角形相似；
（4）两角法：有两组角对应相等的两个三角形相似．
练习册系列答案
海淀黄冈名师导航系列答案
普通高中同步练习册系列答案
相关题目
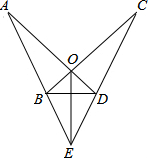如图，AD与BC相交于点O，OA=OC，∠A=∠C，BE=DE．求证：OE垂直平分BD．
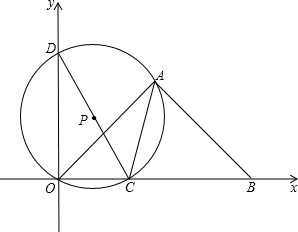如图，等腰三角形ABO的斜边OB在x轴上，O是坐标原点，点A在第一象限内，OB=2，点C是线段OB上一动点（不与O、B重合），△OAC的外接圆P与y轴的另一交点为D，求线段CD长度的最小值．
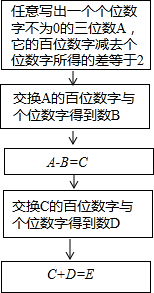阅读右边的框图并回答下列问题：
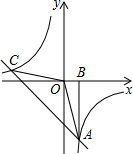如图，已知正比例函数y=kx的图象与反比例函数y=