题目内容
19.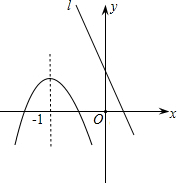 已知抛物线和直线l在同一直角坐标系中的图象如图所示,抛物线的对称轴为直线x=-1,P1(x1,y1),P2(x2,y2)是抛物线上的点,P3(x3,y3)是直线l上的点,且x3<-1<x1<x2,则y1,y2,y3的大小关系是( )
已知抛物线和直线l在同一直角坐标系中的图象如图所示,抛物线的对称轴为直线x=-1,P1(x1,y1),P2(x2,y2)是抛物线上的点,P3(x3,y3)是直线l上的点,且x3<-1<x1<x2,则y1,y2,y3的大小关系是( )| A. | y1<y2<y3 | B. | y2<y3<y1 | C. | y3<y1<y2 | D. | y2<y1<y3 |
分析 设点P0(-1,y0)为抛物线的顶点,根据一次函数的单调性结合抛物线开口向下即可得出y3>y0,再根据二次函数的性质结合二次函数图象即可得出y0>y1>y2,进而即可得出y2<y1<y3,此题得解.
解答 解:设点P0(-1,y0)为抛物线的顶点,
∵抛物线的开口向下,
∴点P0(-1,y0)为抛物线的最高点.
∵直线l上y值随x值的增大而减小,且x3<-1,直线l在抛物线上方,
∴y3>y0.
∵在x>-1上时,抛物线y值随x值的增大而减小,-1<x1<x2,
∴y0>y1>y2,
∴y2<y1<y3.
故选D.
点评 本题考查了二次函数的性质、一次函数的性质以及二次函数的图象,设点P0(-1,y0)为抛物线的顶点,根据一次(二次)函数的性质找出y2<y1<y0<y3是解题的关键.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
9.下列命题中的假命题是( )
| A. | 对顶角相等 | |
| B. | 内错角相等,两直线互相平行 | |
| C. | 同位角相等 | |
| D. | 平行于同一条直线的两直线互相平行 |
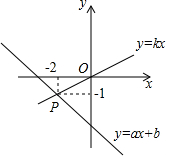 直线y=kx与y=ax+b的图象如图.
直线y=kx与y=ax+b的图象如图.  如图,在正方形ABCD中,AB=12,点E在边CD上,连接AE,将△ADE沿AE翻折,点D落在点F处,点O是对角线BD的中点,连接OF并延长与CD相交于点G,若$\frac{EF}{AB}$=$\frac{1}{3}$,则FG的长度是$\frac{4\sqrt{10}}{5}$.
如图,在正方形ABCD中,AB=12,点E在边CD上,连接AE,将△ADE沿AE翻折,点D落在点F处,点O是对角线BD的中点,连接OF并延长与CD相交于点G,若$\frac{EF}{AB}$=$\frac{1}{3}$,则FG的长度是$\frac{4\sqrt{10}}{5}$.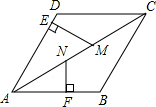 如图,在菱形ABCD中,点M,N在AC上,ME⊥AD,NF⊥AB,若NF=NM=2,ME=3,则AN的长度为4.
如图,在菱形ABCD中,点M,N在AC上,ME⊥AD,NF⊥AB,若NF=NM=2,ME=3,则AN的长度为4.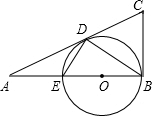 已知:如图,在Rt△ABC中,∠ABC=90°,以AB上的点O为圆心,OB的长为半径的圆与AB交于点E,与AC切于点D.
已知:如图,在Rt△ABC中,∠ABC=90°,以AB上的点O为圆心,OB的长为半径的圆与AB交于点E,与AC切于点D. 如图,△ABC的两条中线AD、CE交于点G,且AD⊥CE.连接BG并延长与AC交于点F,若AD=9,CE=12,则GF为5.
如图,△ABC的两条中线AD、CE交于点G,且AD⊥CE.连接BG并延长与AC交于点F,若AD=9,CE=12,则GF为5. 如图,沿大等腰三角形的对称轴对折,则互相重合的两个小等腰三角形内的单项式的乘积为-4a2b4.
如图,沿大等腰三角形的对称轴对折,则互相重合的两个小等腰三角形内的单项式的乘积为-4a2b4.