题目内容
11.先化简,再求值:(1)2x2+y2+(2y2-3x2)-2(y2-2x2),其中x=-1,y=2
(2)已知|x-1|+(y+2)2=0,求2(3x2y-xy2)-(xy2+6x2y)+1的值.
分析 (1)原式去括号合并得到最简结果,把x与y的值代入计算即可求出值;
(2)利用非负数的性质求出x与y的值,原式去括号合并后代入计算即可求出值.
解答 解:(1)原式=2x2+y2+2y2-3x2-2y2+4x2=3x2+y2,
当x=-1,y=2时,原式=3+4=7;
(2)∵|x-1|+(y+2)2=0,
∴x-1=0,y+2=0,
解得:x=1,y=-2,
则原式=6x2y-2xy2-xy2-6x2y+1=-3xy2+1=-12+1=-11.
点评 此题考查了整式的加减-化简求值,以及非负数的性质:绝对值与偶次方,熟练掌握去括号法则与合并同类项法则是解本题的关键.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案
相关题目
19.下列是最简分式的是( )
| A. | $\frac{12b}{{27{a^2}}}$ | B. | $\frac{{2{{(a-b)}^2}}}{b-a}$ | C. | $\frac{{{x^2}+{y^2}}}{x+y}$ | D. | $\frac{{{x^2}-{y^2}}}{x-y}$ |
3.下列说法错误的是( )
| A. | 频率等于频数与组距比值 | |
| B. | 在频数分布直方图中,频数之和为数据个数 | |
| C. | 在频数分布表中,频率之和为1 | |
| D. | 频率等于频数与样本容量的比值 |
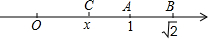 如图所示,数轴上与1,$\sqrt{2}$对应点分别为A,B,点B关于点A的对称点为点C,设点C表示的数为x,求BC的长.
如图所示,数轴上与1,$\sqrt{2}$对应点分别为A,B,点B关于点A的对称点为点C,设点C表示的数为x,求BC的长.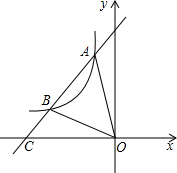 如图,直线y1=kx+b与反比例函数y2=$\frac{k′}{x}$(x<0)的图象相交于点A、点B,与x轴交于点C,其中点A的坐标为(-2,4),点B的横坐标为-4.
如图,直线y1=kx+b与反比例函数y2=$\frac{k′}{x}$(x<0)的图象相交于点A、点B,与x轴交于点C,其中点A的坐标为(-2,4),点B的横坐标为-4.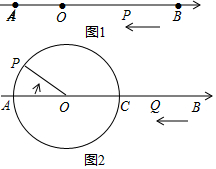 如图1,已知点A,B在以O为原点的数轴上表示的数分别为a,b,且a,b满足|a+4|+(b-10)2=0,动点P从点B出发沿射线BA运动.
如图1,已知点A,B在以O为原点的数轴上表示的数分别为a,b,且a,b满足|a+4|+(b-10)2=0,动点P从点B出发沿射线BA运动.