题目内容
1．
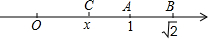如图所示，数轴上与1，$\sqrt{2}$对应点分别为A，B，点B关于点A的对称点为点C，设点C表示的数为x，求BC的长．
分析 根据对称点的坐标公式，可得C点的坐标，根据数轴上两点间的距离是大数减小数，可得答案．
解答 解：设C点坐标为x，
由题意，得
$\frac{x+\sqrt{2}}{2}$=1，
解得x=2-$\sqrt{2}$，BC=$\sqrt{2}$-（2-$\sqrt{2}$）=2$\sqrt{2}$-2．
点评 本题考查了实数与数轴，利用对称点的坐标公式得出C点的坐标是解题关键．
练习册系列答案
相关题目
11．
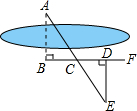如图，要测量河两岸相对的两点A、B的距离，先在AB的垂线BF上取两点C、D，使BC=CD，再作出BF的垂线DE，使点A、C、E在同一条直线上（如图所示），可以说明△ABC≌△EDC，得AB=DE，因此测得DE的长就是AB的长，判定△ABC≌△EDC，最恰当的理由是（ ）
如图，要测量河两岸相对的两点A、B的距离，先在AB的垂线BF上取两点C、D，使BC=CD，再作出BF的垂线DE，使点A、C、E在同一条直线上（如图所示），可以说明△ABC≌△EDC，得AB=DE，因此测得DE的长就是AB的长，判定△ABC≌△EDC，最恰当的理由是（ ）| A． | 边角边 | B． | 角边角 | C． | 边边边 | D． | 边边角 |
已知如图：线段AB=16cm，点C是AB的中点，点D在AC的中点，求线段BD的长．
6．甲乙两辆汽车在一条公路上匀速行驶，为了确定汽车的位置，我们用数轴表示这条公路，并规定向右为正方向，原点O为0km路标．并作如下约定：位置为正，表示汽车位于零千米右侧；位置为负，表示汽车位于零千米左侧，位置为零，表示汽车位于零千米处．
（1）根据题意，填写下列表格：
（2）求出两车的相遇时间．
（1）根据题意，填写下列表格：
| 时间（h） | 0 | 3 | 5 | x |
| 甲车位置（km） | 150 | -30 | -150 | 150-60x |
| 乙车位置（km） | -50 | 70 | 150 | -50+40x |
