题目内容
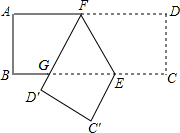 如图,已知在矩形ABCD中,点E在边BC上,BE=2CE,将矩形沿着过点E的直线翻折后,点C、D分别落在边BC下方的点C′、D′处,且点C′、D′、B在同一条直线上,折痕与边AD交于点F,D′F与BE交于点G.设AB=t,那么△EFG的周长为
如图,已知在矩形ABCD中,点E在边BC上,BE=2CE,将矩形沿着过点E的直线翻折后,点C、D分别落在边BC下方的点C′、D′处,且点C′、D′、B在同一条直线上,折痕与边AD交于点F,D′F与BE交于点G.设AB=t,那么△EFG的周长为考点:翻折变换(折叠问题)
专题:几何图形问题,压轴题
分析:根据翻折的性质可得CE=C′E,再根据直角三角形30°角所对的直角边等于斜边的一半判断出∠EBC′=30°,然后求出∠BGD′=60°,根据对顶角相等可得∠FGE=∠∠BGD′=60°,根据两直线平行,内错角相等可得∠AFG=∠FGE,再求出∠EFG=60°,然后判断出△EFG是等边三角形,根据等边三角形的性质表示出EF,即可得解.
解答:解:由翻折的性质得,CE=C′E,
∵BE=2CE,
∴BE=2C′E,
又∵∠C′=∠C=90°,
∴∠EBC′=30°,
∵∠FD′C′=∠D=90°,
∴∠BGD′=60°,
∴∠FGE=∠BGD′=60°,
∵AD∥BC,
∴∠AFG=∠FGE=60°,
∴∠EFG=
(180°-∠AFG)=
(180°-60°)=60°,
∴△EFG是等边三角形,
∵AB=t,
∴EF=t÷
=
t,
∴△EFG的周长=3×
t=2
t.
故答案为:2
t.
∵BE=2CE,
∴BE=2C′E,
又∵∠C′=∠C=90°,
∴∠EBC′=30°,
∵∠FD′C′=∠D=90°,

∴∠BGD′=60°,
∴∠FGE=∠BGD′=60°,
∵AD∥BC,
∴∠AFG=∠FGE=60°,
∴∠EFG=
| 1 |
| 2 |
| 1 |
| 2 |
∴△EFG是等边三角形,
∵AB=t,
∴EF=t÷
| ||
| 2 |
2
| ||
| 3 |
∴△EFG的周长=3×
2
| ||
| 3 |
| 3 |
故答案为:2
| 3 |
点评:本题考查了翻折变换的性质,直角三角形30°角所对的直角边等于斜边的一半,等边三角形的判定与性质,熟记性质并判断出△EFG是等边三角形是解题的关键.

练习册系列答案
相关题目
下列等式中,计算正确的是( )
| A、(2x3)3=6x9 |
| B、x5÷x=x5 |
| C、(-3pq)2=9pq |
| D、a2•a9=a11 |
 甲、乙、丙三人进行飞镖比赛,已知他们每人五次投得的成绩如图,那么三人中成绩最稳定的是
甲、乙、丙三人进行飞镖比赛,已知他们每人五次投得的成绩如图,那么三人中成绩最稳定的是 如图是三种不同类型的地砖,若现有A类4块,B类2块,C类1块,若要拼成一个正方形到还需B类地砖
如图是三种不同类型的地砖,若现有A类4块,B类2块,C类1块,若要拼成一个正方形到还需B类地砖 如图,反比例函数y=
如图,反比例函数y=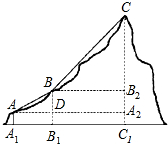 如图,A,B,C表示修建在一座山上的三个缆车站的位置,AB,BC表示连接缆车站的钢缆.已知A,B,C所处位置的海拔AA1,BB1,CC1分别为160米,400米,1000米,钢缆AB,BC分别与水平线AA2,BB2所成的夹角为30°,45°,求钢缆AB和BC的总长度.(结果精确到1米)
如图,A,B,C表示修建在一座山上的三个缆车站的位置,AB,BC表示连接缆车站的钢缆.已知A,B,C所处位置的海拔AA1,BB1,CC1分别为160米,400米,1000米,钢缆AB,BC分别与水平线AA2,BB2所成的夹角为30°,45°,求钢缆AB和BC的总长度.(结果精确到1米)