题目内容
观察下列等式:
第1个等式:a1=
=
-
;
第2个等式:a2=
=
-
;
第3个等式:a3=
=
-
;
第4个等式:a4=
=
-
.
按上述规律,回答以下问题:
(1)用含n的代数式表示第n个等式:an= = ;
(2)式子a1+a2+a3+…+a20= .
第1个等式:a1=
| 3 |
| 1×2×22 |
| 1 |
| 1×2 |
| 1 |
| 2×22 |
第2个等式:a2=
| 4 |
| 2×3×23 |
| 1 |
| 2×22 |
| 1 |
| 3×23 |
第3个等式:a3=
| 5 |
| 3×4×24 |
| 1 |
| 3×23 |
| 1 |
| 4×24 |
第4个等式:a4=
| 6 |
| 4×5×25 |
| 1 |
| 4×24 |
| 1 |
| 5×25 |
按上述规律,回答以下问题:
(1)用含n的代数式表示第n个等式:an=
(2)式子a1+a2+a3+…+a20=
考点:规律型:数字的变化类
专题:规律型
分析:(1)由前四个等是可以看出:是第几个算式,等号左边的分母的第一个因数是就是几,第二个因数是几加1,第三个因数是2的几加1次方,分子是几加2;等号右边分成分子都是1的两项差,第一个分母是几乘2的几次方,第二个分母是几加1乘2的几加1次方;由此规律解决问题;
(2)把这20个数相加,化为左边的形式相加,正好抵消,剩下第一个数分裂的第一项和最后一个数分裂的后一项,得出答案即可.
(2)把这20个数相加,化为左边的形式相加,正好抵消,剩下第一个数分裂的第一项和最后一个数分裂的后一项,得出答案即可.
解答:解:(1)用含n的代数式表示第n个等式:an=
=
-
.
(2)a1+a2+a3+…+a20
=
-
+
-
+
-
+
-
+…+
-
=
-
.
故答案为:(1)
,
-
;
(2)
-
.
| n+2 |
| n(n+1)•2n+1 |
| 1 |
| n•2n |
| 1 |
| (n+1)•2n+1 |
(2)a1+a2+a3+…+a20
=
| 1 |
| 1×2 |
| 1 |
| 2×22 |
| 1 |
| 2×22 |
| 1 |
| 3×23 |
| 1 |
| 3×23 |
| 1 |
| 4×24 |
| 1 |
| 4×24 |
| 1 |
| 5×25 |
| 1 |
| 20×220 |
| 1 |
| 21×221 |
=
| 1 |
| 2 |
| 1 |
| 21×221 |
故答案为:(1)
| n+2 |
| n(n+1)•2n+1 |
| 1 |
| n•2n |
| 1 |
| (n+1)•2n+1 |
(2)
| 1 |
| 2 |
| 1 |
| 21×221 |
点评:此题考查数字的变化规律,从简单情形入手,找出一般规律,利用规律解决问题.

练习册系列答案
相关题目
 如图,在南北方向的海岸线MN上,有A、B两艘巡逻船,现均收到故障船C的求救信号.已知A、B两船相距100(
如图,在南北方向的海岸线MN上,有A、B两艘巡逻船,现均收到故障船C的求救信号.已知A、B两船相距100( 如图,在Rt△ABC中,D,E为斜边AB上的两个点,且BD=BC,AE=AC,则∠DCE的大小为
如图,在Rt△ABC中,D,E为斜边AB上的两个点,且BD=BC,AE=AC,则∠DCE的大小为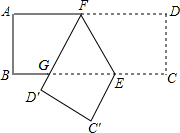 如图,已知在矩形ABCD中,点E在边BC上,BE=2CE,将矩形沿着过点E的直线翻折后,点C、D分别落在边BC下方的点C′、D′处,且点C′、D′、B在同一条直线上,折痕与边AD交于点F,D′F与BE交于点G.设AB=t,那么△EFG的周长为
如图,已知在矩形ABCD中,点E在边BC上,BE=2CE,将矩形沿着过点E的直线翻折后,点C、D分别落在边BC下方的点C′、D′处,且点C′、D′、B在同一条直线上,折痕与边AD交于点F,D′F与BE交于点G.设AB=t,那么△EFG的周长为 如图,点E在DF上,点B在AC上,∠1=∠2,∠C=∠D.试说明:AC∥DF.
如图,点E在DF上,点B在AC上,∠1=∠2,∠C=∠D.试说明:AC∥DF.