题目内容
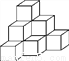
用棱长是1cm的小正方体组成如图所示的几何体,把这个几何体放在桌子上,并把暴露的面涂上颜色,那么涂颜色面的面积之和是____cm2.
练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案
相关题目
题目内容
用棱长是1cm的小正方体组成如图所示的几何体,把这个几何体放在桌子上,并把暴露的面涂上颜色,那么涂颜色面的面积之和是____cm2.

 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案