题目内容
 如图,在平面直角坐标系xOy中,A、B为x轴上两点,C、D为y轴上两点,经过点A、C、B的抛物线的一部分了C1经过点A、D、B的抛物线的一部分C2组成一条封闭曲线,已知点C的坐标为(0,-1.5),M是抛物线C2;y=tx2-2tx-3t(t<0)的顶点.
如图,在平面直角坐标系xOy中,A、B为x轴上两点,C、D为y轴上两点,经过点A、C、B的抛物线的一部分了C1经过点A、D、B的抛物线的一部分C2组成一条封闭曲线,已知点C的坐标为(0,-1.5),M是抛物线C2;y=tx2-2tx-3t(t<0)的顶点.(1)求抛物线C1的解析式;
(2)在第四象限的封闭曲线上确定一点P,使△PBC面积最大,求出此时△PBC的最大值;
(3)是否存在t值使得SS△BCD=2S△ACM?若存在,求出t的值;若不存在,请说明理由.
考点:二次函数综合题
专题:
分析:(1)令y=0,则tx2-2tx-3t=0,根据t<0,可得出x2-2x-3=0A(-1,0),B(3,0),设抛物线C1的表达式为y=a(x+1)(x-3)(a≠0),把点C代入求出a的值,进而得出结论;
(2)根据S△PBC=S△POC+S△BOP-S△BOC就可得出结论;
(3)由D,M的坐标求出C、D的长,故可得出△BCD的面积,连接AM,交y轴于点E,直线AM的方程为y=-2tx-2t,2S△ACM=-4t+3,再由S△BCD=2S△ACM,即可得出结论.
(2)根据S△PBC=S△POC+S△BOP-S△BOC就可得出结论;
(3)由D,M的坐标求出C、D的长,故可得出△BCD的面积,连接AM,交y轴于点E,直线AM的方程为y=-2tx-2t,2S△ACM=-4t+3,再由S△BCD=2S△ACM,即可得出结论.
解答: 解:(1)令y=0,则tx2-2tx-3t=0,
解:(1)令y=0,则tx2-2tx-3t=0,
∵t<0,
∴x2-2x-3=0,解得x1=-1,x2=3,
∴A(-1,0),B(3,0),
∵设抛物线C1的表达式为y=a(x+1)(x-3)(a≠0),把C(0,-
)代入得,a=
,
∴抛物线C1的表达式为y=
x2-x-
;
(2)∵设P(p,
x2-x-
),
∴S△PBC=S△POC+S△BOP-S△BOC=-
(p-
)2+
,
∴当p=
时,△PBC的面积最大值为
;
(3)∵由C2知D(0,-3t),M(1,-4t),
∴CD=-3t+
,
∴S△BCD=
CD•OB=-
t+
,
连接AM,交y轴于点E,直线AM的方程为y=-2tx-2t,
∴E(0,-20),CE=-2t+
,
∴S△ACM=-2t+
,
∴2S△ACM=-4t+3,
∵S△BCD=2S△ACM,解得t=-
.
 解:(1)令y=0,则tx2-2tx-3t=0,
解:(1)令y=0,则tx2-2tx-3t=0,∵t<0,
∴x2-2x-3=0,解得x1=-1,x2=3,
∴A(-1,0),B(3,0),
∵设抛物线C1的表达式为y=a(x+1)(x-3)(a≠0),把C(0,-
| 3 |
| 2 |
| 1 |
| 2 |
∴抛物线C1的表达式为y=
| 1 |
| 2 |
| 3 |
| 2 |
(2)∵设P(p,
| 1 |
| 2 |
| 3 |
| 2 |
∴S△PBC=S△POC+S△BOP-S△BOC=-
| 3 |
| 4 |
| 3 |
| 2 |
| 27 |
| 16 |
∴当p=
| 3 |
| 2 |
| 27 |
| 16 |
(3)∵由C2知D(0,-3t),M(1,-4t),
∴CD=-3t+
| 3 |
| 2 |
∴S△BCD=
| 3 |
| 2 |
| 9 |
| 2 |
| 9 |
| 4 |
连接AM,交y轴于点E,直线AM的方程为y=-2tx-2t,
∴E(0,-20),CE=-2t+
| 3 |
| 2 |
∴S△ACM=-2t+
| 3 |
| 2 |
∴2S△ACM=-4t+3,
∵S△BCD=2S△ACM,解得t=-
| 3 |
| 2 |
点评:本题考查的是二次函数综合题,涉及到二次函数的性质、用待定系数法求一次函数及二次函数的解析式等知识,难度较大.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,边长为6的大正方形中有两个小正方形,若两个小正方形的面积分别为S1、S2,则k=
如图,边长为6的大正方形中有两个小正方形,若两个小正方形的面积分别为S1、S2,则k=| s2+s1 |
| s2-s1 |
| A、16 | B、17 | C、18 | D、19 |
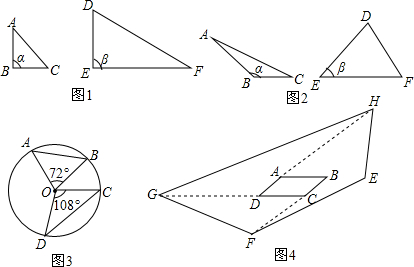
 如图,在△ABC中AB=AC,∠A=56°,BD⊥AC于D,求∠CBD的度数.
如图,在△ABC中AB=AC,∠A=56°,BD⊥AC于D,求∠CBD的度数.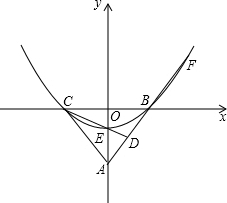 如图,在平面直角坐标系中xoy中,AO=8,AB=AC,sin∠ABC=
如图,在平面直角坐标系中xoy中,AO=8,AB=AC,sin∠ABC=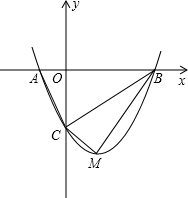 如图,抛物线y=mx2-2mx-3m(m>0)与x轴交与A、B两点,与y轴交与C点.
如图,抛物线y=mx2-2mx-3m(m>0)与x轴交与A、B两点,与y轴交与C点. 如图,AD是△ABC的角平分线,DE∥AB交AC于点E,AB=8,AC=6,则DE=
如图,AD是△ABC的角平分线,DE∥AB交AC于点E,AB=8,AC=6,则DE=