题目内容
20．某足球运动员在离球门6m处抬脚劲射，足球沿抛物线形的路线运行，当球运行的水平距离为4m时达到最大高度为3.2m，已知球门的横梁高2.44m，问此球有进球门的可能吗？分析 首先建立直角坐标系，顶点为（4，3.2），起点为（0，0）．设抛物线的解析式为y=a（x-4）2+3.2，求出a的值．再代入x的值后易求出y的值．
解答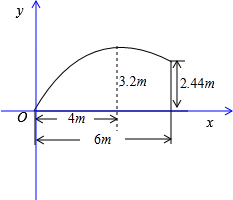 
解：如图，建立直角坐标系，
球飞行的路线为抛物线，顶点（4，3.2），起点（0，0），
设抛物线的解析式为y=a（x-4）2+3.2，
∴0=a（0-4）2+3.2，
∴a=-$\frac{1}{5}$；
∴抛物线的解析式为y=-$\frac{1}{5}$（x-4）2+3.2，
当x=6时，y=2.4＜2.44，
故运动员这一脚能射中球门．
点评 本题考查点的坐标的求法及二次函数的实际应用．此题为数学建模题，借助二次函数解决实际问题．
练习册系列答案
作业辅导系列答案
相关题目
8．下列关系式中，属于二次函数的是（x为自变量）（ ）
| A． | y=ax2+bx+c | B． | $y=\sqrt{{x^2}-1}$ | C． | $y=\frac{1}{x^2}$ | D． | $y=\frac{1}{8}{x^2}$ |
15．若132x=64，则13-x=（ ）
| A． | -$\frac{1}{8}$ | B． | ±$\frac{1}{8}$ | C． | $\frac{1}{80}$ | D． | $\frac{1}{512}$ |
5．若分式$\frac{{x}^{2}-1}{x-1}$的值为0，则x的取值为（ ）
| A． | x=1 | B． | x=-1 | C． | x=±1 | D． | 无法确定 |
9．一台电冰箱的原价是2400元，现在按七折出售，求现价多少元？列式是（ ）
| A． | 2400÷70% | B． | 2400×70% | C． | 2400×（1-70%） | D． | 2400×7 |
10．下列等式不成立的是（ ）
| A． | 6$\sqrt{2}$×$\sqrt{3}=6$$\sqrt{6}$ | B． | $\sqrt{8}$$÷\sqrt{2}=2$ | C． | $\frac{1}{\sqrt{3}}=\frac{\sqrt{3}}{3}$ | D． | $\sqrt{8}-\sqrt{2}=2$ |