题目内容
1.设方程x2-3x+1=0两根为x1,x2,则x12+3x2的值为8.分析 根据方程解的定义和根与系数的关系由x1、x2是方程x2-3x+1=0的两实根得到x12-3x1+1=0,x1+x2=3,则x12=3x1-1,于是x12+3x2可化为3x1+3x2-1=3(x1+x2)-1,然后把x1+x2=3代入计算即可.
解答 解:∵x1是方程x2-3x+1=0的根,
∴x12-3x1+1=0,即x12=3x1-1,
∴x12+3x2=3x1+3x2=3(x1+x2)-1,
∵x1、x2是方程x2-3x+1=0的两实根,
∴x1+x2=3,
∴x12+3x2=3(x1+x2)-1=3×3-1=8.
故答案为8.
点评 本题主要考查了根与系数的关系以及一元二次方程的解的知识,解答本题的关键是把是x12+3x2可化为3x1+3x2-1=3(x1+x2)-1,此题难度不大.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12. 下面几何体的主视图是( )
下面几何体的主视图是( )
 下面几何体的主视图是( )
下面几何体的主视图是( )| A. |  | B. |  | C. |  | D. |  |
16.二次函数y=-x2+4与y轴的交点坐标是( )
| A. | (0,-2) | B. | (0,2) | C. | (0,-4) | D. | (0,4) |
6.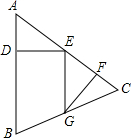 如图,在△ABC中,点E在AC上,点G在BC上,连接EG,AE=EG=5,过点E作ED⊥AB,垂足为D,过点G作GF⊥AC,垂足为F,此时恰有DE=GF=4.若BG=2$\sqrt{5}$,则sinB的值为( )
如图,在△ABC中,点E在AC上,点G在BC上,连接EG,AE=EG=5,过点E作ED⊥AB,垂足为D,过点G作GF⊥AC,垂足为F,此时恰有DE=GF=4.若BG=2$\sqrt{5}$,则sinB的值为( )
 如图,在△ABC中,点E在AC上,点G在BC上,连接EG,AE=EG=5,过点E作ED⊥AB,垂足为D,过点G作GF⊥AC,垂足为F,此时恰有DE=GF=4.若BG=2$\sqrt{5}$,则sinB的值为( )
如图,在△ABC中,点E在AC上,点G在BC上,连接EG,AE=EG=5,过点E作ED⊥AB,垂足为D,过点G作GF⊥AC,垂足为F,此时恰有DE=GF=4.若BG=2$\sqrt{5}$,则sinB的值为( )| A. | $\frac{2\sqrt{5}}{10}$ | B. | $\frac{\sqrt{5}}{10}$ | C. | $\frac{2\sqrt{5}}{5}$ | D. | $\frac{\sqrt{5}}{5}$ |
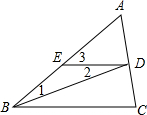 如图,填空:已知BD平分∠ABC,ED∥BC,∠1=20°.
如图,填空:已知BD平分∠ABC,ED∥BC,∠1=20°. 如图,平面直角坐标系中,直线AB分别交x轴正半轴于点A,交y轴正半轴于点B,且OA、OB(OA<OB)的长是方程x2-12x+32=0的两个根.
如图,平面直角坐标系中,直线AB分别交x轴正半轴于点A,交y轴正半轴于点B,且OA、OB(OA<OB)的长是方程x2-12x+32=0的两个根.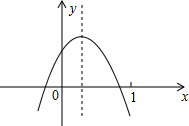 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论:其中正确的有( )
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论:其中正确的有( )