题目内容
11.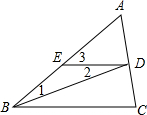 如图,填空:已知BD平分∠ABC,ED∥BC,∠1=20°.
如图,填空:已知BD平分∠ABC,ED∥BC,∠1=20°.∵BD平分∠ABC,
∴∠CBD=∠1=20°,
又∵ED∥BC,
∴∠2=∠CBD=20°.
理由是:两直线平行,内错角相等.
又由BD平分∠ABC,
可知∠ABC=2∠1=40°.
又∵ED∥BC,
∴∠3=∠ABC=40°.
理由是:两直线平行,同位角相等.
分析 根据角平分线的定义,两直线平行,内错角相等和两直线平行,同位角相等解答.
解答 解:∵BD平分∠ABC,
∴∠CBD=∠1=20°,
又∵ED∥BC,
∴∠2=∠CBD=20°.
理由是:两直线平行,内错角相等.
又由BD平分∠ABC,
可知∠ABC=2∠1=40°.
又∵ED∥BC,
∴∠3=∠ABC=40°.
理由是:两直线平行,同位角相等.
故答案为:∠CBD;∠CBD;20;两直线平行,内错角相等;2∠1;40;∠ABC;40;两直线平行,同位角相等.
点评 本题考查了平行线的性质,角平分线的定义,主要是逻辑推理能力的训练,是基础题,熟记性质是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
6. 实数a、b在数轴上的位置如图所示,则下列式子成立的是( )
实数a、b在数轴上的位置如图所示,则下列式子成立的是( )
 实数a、b在数轴上的位置如图所示,则下列式子成立的是( )
实数a、b在数轴上的位置如图所示,则下列式子成立的是( )| A. | a+b>0 | B. | a+b<0 | C. | a>-b | D. | -a<b |
3.多项式x2y2-y2-x2+1因式分解的结果是( )
| A. | (x2+1)(y2+1) | B. | (x-1)(x+1)(y2+1) | C. | (x2+1)(y+1)(y-1) | D. | (x+1)(x-1)(y+1)(y-1) |
20.-6是( )
| A. | 负有理数 | B. | 正有理数 | C. | 自然数 | D. | 无理数 |
 如图,用8块相同的长方形拼成一个宽为48厘米的大长方形,则每块小长方形的长和宽分别是33厘米和15厘米.
如图,用8块相同的长方形拼成一个宽为48厘米的大长方形,则每块小长方形的长和宽分别是33厘米和15厘米.