题目内容
6.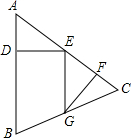 如图,在△ABC中,点E在AC上,点G在BC上,连接EG,AE=EG=5,过点E作ED⊥AB,垂足为D,过点G作GF⊥AC,垂足为F,此时恰有DE=GF=4.若BG=2$\sqrt{5}$,则sinB的值为( )
如图,在△ABC中,点E在AC上,点G在BC上,连接EG,AE=EG=5,过点E作ED⊥AB,垂足为D,过点G作GF⊥AC,垂足为F,此时恰有DE=GF=4.若BG=2$\sqrt{5}$,则sinB的值为( )| A. | $\frac{2\sqrt{5}}{10}$ | B. | $\frac{\sqrt{5}}{10}$ | C. | $\frac{2\sqrt{5}}{5}$ | D. | $\frac{\sqrt{5}}{5}$ |
分析 首先证明Rt△ADE≌Rt△EFG,推出∠DEG为直角;然后过点G作GH⊥AB于点H,则四边形DEGH为矩形;最后在Rt△BGH中,利用三角函数定义求出sinB的值.
解答 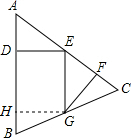 解:在Rt△ADE与Rt△EFG中,
解:在Rt△ADE与Rt△EFG中,
$\left\{\begin{array}{l}AE=EG\\ DE=GF\end{array}\right.$
∴Rt△ADE≌Rt△EFG(HL).
∴∠A=∠GEF.
∵∠A+∠AED=90°,
∴∠GEF+∠AED=90°,
∴∠DEG=90°.
如右图,过点G作GH⊥AB于点H,则四边形DEGH为矩形,
∴GH=DE=4.
在Rt△BGH中,sinB=$\frac{GH}{BG}$=$\frac{4}{2\sqrt{5}}$=$\frac{2\sqrt{5}}{5}$.
故选C.
点评 本题是几何综合题,考查了全等三角形、矩形的判定与性质,三角函数的定义.注意辅助线的作法.

练习册系列答案
相关题目
16.和温带大陆性气候相比较,温带海洋性气候地区每天气温变化的幅度比较小,较适合人类居住,所以温带海洋性气候地区每天气温的( )比较小.
| A. | 极差 | B. | 平均数 | C. | 众数 | D. | 中位数 |

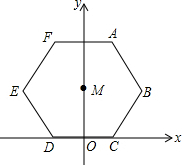 如图,一个边长为2的正六边形ABCDEF的边CD在x轴上,正六边形的中心M在y轴上,现在把这个正六边形沿x轴无滑动的滚动一周,则顶点A的坐标为(13,2$\sqrt{3}$),若滚动100周,中心M经过的路径长400π.
如图,一个边长为2的正六边形ABCDEF的边CD在x轴上,正六边形的中心M在y轴上,现在把这个正六边形沿x轴无滑动的滚动一周,则顶点A的坐标为(13,2$\sqrt{3}$),若滚动100周,中心M经过的路径长400π.