题目内容
如果
＜
＜
，p，q是正整数，则p的最小值是（ ）
| 7 |
| 8 |
| q |
| p |
| 8 |
| 9 |
| A、15 | B、17 | C、72 | D、144 |
考点：有理数无理数的概念与运算
专题：计算题
分析：根据不等式先写出q的取值范围，根据q为正整数，结合选项判断p的最小值．
解答：解：由题意得，
p＜q＜
p，
如果p=15，则此时13.325＜q＜13.33，q没有正整数值；
如果p=17，则此时14.875＜q＜15.111，q可取15；
如果p=72，则此时63＜q＜64，q没有正整数值；
如果p=144，则此时126＜q＜128，q可取127；
综上可得p的最小值为17．
故选B．
| 7 |
| 8 |
| 8 |
| 9 |
如果p=15，则此时13.325＜q＜13.33，q没有正整数值；
如果p=17，则此时14.875＜q＜15.111，q可取15；
如果p=72，则此时63＜q＜64，q没有正整数值；
如果p=144，则此时126＜q＜128，q可取127；
综上可得p的最小值为17．
故选B．
点评：此题考查了有理数无理数的概念与运算，解答本题的关键是将原不等式进行转换，因为是选择题，我们可以将选项代入判断．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
锐角三角形△ABC中，∠C=2∠B，则∠B的范围是（ ）
| A、10°＜∠B＜20° |
| B、20°＜∠B＜30° |
| C、30°＜∠B＜45° |
| D、45°＜∠B＜60° |
在平行四边形ABCD中，下列结论中正确的是（ ）
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
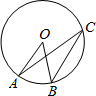如图，点O是⊙O的圆心，点A、B、C在⊙O上，AO∥BC，∠AOB=40°，则∠OAC的度数等于（ ）| A、40° | B、60° |
| C、50° | D、20° |