题目内容
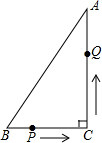 如图,在△ABC中,∠C=90°,BC=7cm,AC=24cm,P点在BC上,从B点到C点运动(不包括C点),点P运动的速度为2cm/s;Q点在AC上从C点运动到A点(不包括A点),速度为5cm/s.若点P、Q分别从B、C同时运动,设经过了x秒,请解答下面的问题,并写出探索的主要过程:
如图,在△ABC中,∠C=90°,BC=7cm,AC=24cm,P点在BC上,从B点到C点运动(不包括C点),点P运动的速度为2cm/s;Q点在AC上从C点运动到A点(不包括A点),速度为5cm/s.若点P、Q分别从B、C同时运动,设经过了x秒,请解答下面的问题,并写出探索的主要过程:(1)PC=
(2)经过多少时间,△PCQ的面积为15cm2;
(3)经过多少时间,△PCQ的面积最大,最大面积是多少?
考点:一元二次方程的应用,二次函数的最值
专题:几何动点问题
分析:(1)利用x表示出PC、CQ的长,依此即可求解
(2)设运动时间为x秒,根据三角形的面积公式表示出△PCQ的面积,令其等于15即可列出关于x的方程,解方程即可;
(3)利用(2)中所求表达式,根据二次函数的性质求出最大值即可.
(2)设运动时间为x秒,根据三角形的面积公式表示出△PCQ的面积,令其等于15即可列出关于x的方程,解方程即可;
(3)利用(2)中所求表达式,根据二次函数的性质求出最大值即可.
解答:解:(1)PC=(7-2x)cm,QC=5xcm;
(2)依题意得:
(7-2x)•5x=15…(3分)
整理得:2x2-7x+6=0
解得:x1=
,x2=2
经检验,x1=
,x2=2符合题意
答:经过
秒或2秒,△PCQ的面积为15cm2;
(3)设△PCQ的面积为S
则S=
(7-2x)•5x=-5(x-
)2+
∵0≤x<
∴当x=
时,△PCQ的面积最大,最大面积是
.
故答案为:(7-2x);5x.
(2)依题意得:
| 1 |
| 2 |
整理得:2x2-7x+6=0
解得:x1=
| 3 |
| 2 |
经检验,x1=
| 3 |
| 2 |
答:经过
| 3 |
| 2 |
(3)设△PCQ的面积为S
则S=
| 1 |
| 2 |
| 7 |
| 4 |
| 245 |
| 16 |
∵0≤x<
| 7 |
| 2 |
∴当x=
| 7 |
| 4 |
| 245 |
| 16 |
故答案为:(7-2x);5x.
点评:本题考查了一元二次方程的应用、二次函数的最值及三角形的面积,用时间表示出三角形各边长度是解题的关键.

练习册系列答案
相关题目
 已知A、B在数轴上分别表示a、b
已知A、B在数轴上分别表示a、b 已知如图,△ABC≌△DCB,其中的:
已知如图,△ABC≌△DCB,其中的: