题目内容
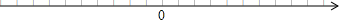 已知A、B在数轴上分别表示a、b
已知A、B在数轴上分别表示a、b(1)对照数轴填写下表:
| a | 6 | -6 | -6 | 2 | -1.5 |
| b | 4 | 0 | -4 | -10 | -1.5 |
| A、B两点的距离 | 2 | 0 |
(3)在数轴上标出所有符合条件的整数点P,使它到10和-10的距离之和为20,并求所有这些整数的和.
(4)找出(3)中满足到10和-10的距离之差大于1而小于5的整数的点P.
(5)若点C表示的数为x,当C在什么位置时,|x+1|+|x-2|取得的值最小?
考点:数轴,绝对值
专题:
分析:(1)根据数轴的知识,结合表格中的数即可得出答案.
(2)由(1)所填写的数字,即可得出结论.
(3)由数轴的知识,可得出只要在-10和10之间的整数均满足题意.
(4)根据(3)的式子即可得到结果;
(5)根据绝对值的几何意义,可得出-1和2之间的任何一点均满足题意.
(2)由(1)所填写的数字,即可得出结论.
(3)由数轴的知识,可得出只要在-10和10之间的整数均满足题意.
(4)根据(3)的式子即可得到结果;
(5)根据绝对值的几何意义,可得出-1和2之间的任何一点均满足题意.
解答:解:(1)填表如下:
(2)由(1)可得:d=|a-b|或d=|b-a|;
(3)只要在-10和10之间的整数均满足到-10和10的距离之和为20,有:-10、-9、-8、-7、-6、-5、-4、-3、-2、-1、0、1、2、3、4、5、6、7、8、9、10,
所有满足条件的整数之和为:-10+(-9)+(-8)+(-7)+(-6)+(-5)+(-4)+(-3)+(-2)+(-1)+0+1+2+3+4+5+6+7+8+9+10=0;
(4)-2,-1
(5)根据数轴的几何意义可得-1和2之间的任何一点均能使|x+1|+|x-2|取得的值最小.
故可得:点C的范围在:-1≤x≤2时,能满足题意.
| a | 6 | -6 | -6 | 2 | -1.5 |
| b | 4 | 0 | -4 | -10 | -1.5 |
| A、B两点的距离 | 2 | 6 | 2 | 12 | 0 |
(3)只要在-10和10之间的整数均满足到-10和10的距离之和为20,有:-10、-9、-8、-7、-6、-5、-4、-3、-2、-1、0、1、2、3、4、5、6、7、8、9、10,
所有满足条件的整数之和为:-10+(-9)+(-8)+(-7)+(-6)+(-5)+(-4)+(-3)+(-2)+(-1)+0+1+2+3+4+5+6+7+8+9+10=0;
(4)-2,-1
(5)根据数轴的几何意义可得-1和2之间的任何一点均能使|x+1|+|x-2|取得的值最小.
故可得:点C的范围在:-1≤x≤2时,能满足题意.
点评:本题主要考查数轴和数的绝对值,解答本题的关键是理解绝对值的几何意义,借助数轴解决问题.

练习册系列答案
相关题目
 已知△ABC和△DEF都是边长为10cm的等边三角形,且BCDE在同一直线上,连接AD、CF.若BD=3cm,△ABC沿着BE的方向以每秒1cm的速度运动,设△ABC运动时间为t.
已知△ABC和△DEF都是边长为10cm的等边三角形,且BCDE在同一直线上,连接AD、CF.若BD=3cm,△ABC沿着BE的方向以每秒1cm的速度运动,设△ABC运动时间为t. 如图,AD与BC相交于O,OC=OD,OA=OB,求证:∠CAB=∠DBA.
如图,AD与BC相交于O,OC=OD,OA=OB,求证:∠CAB=∠DBA.
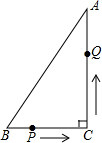 如图,在△ABC中,∠C=90°,BC=7cm,AC=24cm,P点在BC上,从B点到C点运动(不包括C点),点P运动的速度为2cm/s;Q点在AC上从C点运动到A点(不包括A点),速度为5cm/s.若点P、Q分别从B、C同时运动,设经过了x秒,请解答下面的问题,并写出探索的主要过程:
如图,在△ABC中,∠C=90°,BC=7cm,AC=24cm,P点在BC上,从B点到C点运动(不包括C点),点P运动的速度为2cm/s;Q点在AC上从C点运动到A点(不包括A点),速度为5cm/s.若点P、Q分别从B、C同时运动,设经过了x秒,请解答下面的问题,并写出探索的主要过程: