题目内容
已知关于x的方程x2+2(a-1)x+a2-7a-4有两个不相等的实根为x1、x2,且满足x1x2-3x1-3x2-2=0.则a的值是( )
| A、-3 | B、4 | C、-3或4 | D、1 |
考点:根与系数的关系,根的判别式
专题:计算题
分析:先由方程x2+2(a-1)x+a2-7a-4有两个不相等的实根,根据△的意义得到△=4(a-1)2-4(a2-7a-4)=20a+20>0,可解得a>-1,然后根据根与系数的关系得
x1+x2=-2(a-1),x1•x2=a2-7a-4,由已知足x1x2-3x1-3x2-2=0,变形得x1x2-3(x1+x2)-2=0,再把x1+x2=-2(a-1),x1•x2=a2-7a-4代入得到关于a的一元二次方程a2-a-12=0,解得a1=4,a2=-3,而a≥-1,即可得到a=4.
x1+x2=-2(a-1),x1•x2=a2-7a-4,由已知足x1x2-3x1-3x2-2=0,变形得x1x2-3(x1+x2)-2=0,再把x1+x2=-2(a-1),x1•x2=a2-7a-4代入得到关于a的一元二次方程a2-a-12=0,解得a1=4,a2=-3,而a≥-1,即可得到a=4.
解答:解:∵关于x的方程x2+2(a-1)x+a2-7a-4有两个不相等的实根为x1、x2,
∴△=4(a-1)2-4(a2-7a-4)=20a+20>0,解得a>-1,
∴x1+x2=-2(a-1),x1•x2=a2-7a-4,
而x1x2-3x1-3x2-2=0,即x1x2-3(x1+x2)-2=0,
∴a2-7a-4+6(a-1)-2=0,a2-a-12=0,解得a1=4,a2=-3,
∴a=4.
故选B.
∴△=4(a-1)2-4(a2-7a-4)=20a+20>0,解得a>-1,
∴x1+x2=-2(a-1),x1•x2=a2-7a-4,
而x1x2-3x1-3x2-2=0,即x1x2-3(x1+x2)-2=0,
∴a2-7a-4+6(a-1)-2=0,a2-a-12=0,解得a1=4,a2=-3,
∴a=4.
故选B.
点评:本题考查了一元二次方程ax2+bx+c=0(a≠0)的根与系数的关系:若方程的两根分别为x1,x2,则x1+x2=-
,x1•x2=
.也考查了一元二次方程ax2+bx+c=0(a≠0)的根的判别式以及解一元二次方程.
| b |
| a |
| c |
| a |

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
不等式组
的解集在数轴上表示正确的是( )
|
A、 |
B、 |
C、 |
D、 |
某校初三•一班学生参加体育加试,第一小组引体向上的成绩如下表所示:
则这组学生引体向上个数的众数和中位数分别为( )
| 引体向上的个数 | 7 | 8 | 9 | 10 |
| 人数 | 2 | 1 | 4 | 5 |
| A、9.5和10 |
| B、9和10 |
| C、10和9.5 |
| D、10和9 |
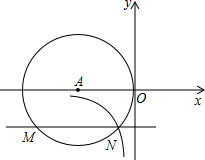 如图,在平面直角坐标系中,⊙A与y轴相切于原点O,平行于x轴的直线交⊙O于M、N两点,若点M的坐标是(-4,-2),过点N的双曲线是
如图,在平面直角坐标系中,⊙A与y轴相切于原点O,平行于x轴的直线交⊙O于M、N两点,若点M的坐标是(-4,-2),过点N的双曲线是 如图所示平行四边形ABCD中,E是BC上一点,且
如图所示平行四边形ABCD中,E是BC上一点,且