题目内容
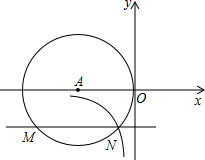 如图,在平面直角坐标系中,⊙A与y轴相切于原点O,平行于x轴的直线交⊙O于M、N两点,若点M的坐标是(-4,-2),过点N的双曲线是y=
如图,在平面直角坐标系中,⊙A与y轴相切于原点O,平行于x轴的直线交⊙O于M、N两点,若点M的坐标是(-4,-2),过点N的双曲线是y=| k |
| x |
考点:反比例函数综合题
专题:
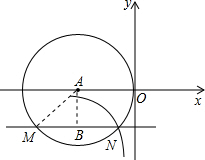
分析:过A点作AB⊥MN,垂足为B,连接AM,设⊙A的半径为r,则BM=4-r,由垂径定理可知MB=BN,在Rt△ABM中,由勾股定理求r的值,确定N点坐标,再代入双曲线解析式即可.
解答:解:如图,过A点作AB⊥MN,垂足为B,连接AM,
设⊙A的半径为r,则BM=4-r,
在Rt△ABM中,AM=r,AB=2,
由勾股定理,得AB2+BM2=AM2,
即22+(4-r)2=r2,解得r=
,BM=4-r=
,
由垂径定理,得BN=BM=
,
即MN=2BM=3,故N(-1,-2),
而N点在双曲线y=
上,
故k=xy=2,
故答案为:2.
设⊙A的半径为r,则BM=4-r,
在Rt△ABM中,AM=r,AB=2,
由勾股定理,得AB2+BM2=AM2,
即22+(4-r)2=r2,解得r=
| 5 |
| 2 |
| 3 |
| 2 |
由垂径定理,得BN=BM=
| 3 |
| 2 |
即MN=2BM=3,故N(-1,-2),
而N点在双曲线y=
| k |
| x |
故k=xy=2,
故答案为:2.

点评:本题考查了反比例函数的综合运用.关键是作弦的垂线,连接半径,构造直角三角形求半径,根据垂径定理,勾股定理求半径,用线段长表示N点坐标.

练习册系列答案
相关题目
 如图,BD是⊙O的直径,∠A=62°,则sin∠CBD的值( )
如图,BD是⊙O的直径,∠A=62°,则sin∠CBD的值( )A、大于
| ||
B、等于
| ||
C、小于
| ||
| D、二者不可比较 |
 如图,在梯形ABCD中,AD∥BC,AB=DC,点O为底边AD的中点.求证:OB=OC (要求:写出证明过程中的重要依据)
如图,在梯形ABCD中,AD∥BC,AB=DC,点O为底边AD的中点.求证:OB=OC (要求:写出证明过程中的重要依据)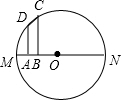 如图,梯形ABCD中,AD∥BC,∠ABC=90°,AD=2,AB=1,BC=3.若此梯形的顶点A、B恰好在圆O的直径MN上,C、D在圆O上,则圆O的直径等于
如图,梯形ABCD中,AD∥BC,∠ABC=90°,AD=2,AB=1,BC=3.若此梯形的顶点A、B恰好在圆O的直径MN上,C、D在圆O上,则圆O的直径等于