题目内容
 如图所示平行四边形ABCD中,E是BC上一点,且
如图所示平行四边形ABCD中,E是BC上一点,且| BE |
| EC |
| 2 |
| 3 |
考点:相似三角形的判定与性质,平行四边形的性质
专题:
分析:由四边形ABCD是平行四边形,可得AD∥BC,AD=BC,继而可判定△BEF∽△DAF,根据相似三角形的对应边成比例,即可得BF:DF=BE:AD,又由
=
,即可得BF:DF=2:5,又由BF=5,即可求得BD的值.
| BE |
| EC |
| 2 |
| 3 |
解答:解:∵
=
,
∴
=
,
∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴△BEF∽△DAF,BE:AD=2:5,
∴BF:DF=BE:AD=2:5,
∵BF=5,
∴DF=
,
∴BD=BF+DF=5+
=
.
故答案为:
.
| BE |
| EC |
| 2 |
| 3 |
∴
| BE |
| BC |
| 2 |
| 5 |
∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴△BEF∽△DAF,BE:AD=2:5,
∴BF:DF=BE:AD=2:5,
∵BF=5,
∴DF=
| 25 |
| 2 |
∴BD=BF+DF=5+
| 25 |
| 2 |
| 35 |
| 2 |
故答案为:
| 35 |
| 2 |
点评:此题考查了相似三角形的判定与性质与平行四边形的性质.此题比较简单,解题的关键是根据题意判定△BEF∽△DAF,再利用相似三角形的对应边成比例定理求解.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
 如图,△ABC中,∠ABC=90°,∠BAC=30°,△ABD、△ACE都是等边三角形,M为CE边中点,DM交AB于点N.求证:AN=NB.
如图,△ABC中,∠ABC=90°,∠BAC=30°,△ABD、△ACE都是等边三角形,M为CE边中点,DM交AB于点N.求证:AN=NB. 如图是一组数据的折线统计图,这组数据的方差是
如图是一组数据的折线统计图,这组数据的方差是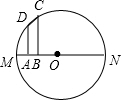 如图,梯形ABCD中,AD∥BC,∠ABC=90°,AD=2,AB=1,BC=3.若此梯形的顶点A、B恰好在圆O的直径MN上,C、D在圆O上,则圆O的直径等于
如图,梯形ABCD中,AD∥BC,∠ABC=90°,AD=2,AB=1,BC=3.若此梯形的顶点A、B恰好在圆O的直径MN上,C、D在圆O上,则圆O的直径等于