题目内容
7.已知二次函数y=mx2+x-1的图象与x轴有两个交点,则m的取值范围是( )| A. | m>-$\frac{1}{4}$ | B. | m≥-$\frac{1}{4}$ | C. | m>-$\frac{1}{4}$且m≠0 | D. | m≥-$\frac{1}{4}$且m≠0 |
分析 根据二次函数y=mx2+x-1的图象与x轴有两个交点,可得△=12-4m×(-1)>0且m≠0.
解答 解:∵原函数是二次函数,
∴m≠0.
∵二次函数y=mx2+x-1的图象与x轴有两个交点,则
△=b2-4ac>0,
△=12-4m×(-1)>0,
∴m>-$\frac{1}{4}$.
综上所述,m的取值范围是:m>-$\frac{1}{4}$且m≠0,
故选C.
点评 本题考查了抛物线与x轴的交点,关键是熟记当△=b2-4ac>0时图象与x轴有两个交点;当△=b2-4ac=0时图象与x轴有一个交点;当△=b2-4ac<0时图象与x轴没有交点.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.二次函数y=ax2+bx+c对于x的任何值都恒为负值的条件是( )
| A. | a>0,△>0 | B. | a>0,△<0 | C. | a<0,△>0 | D. | a<0,△<0 |
2.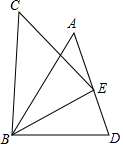 如图,已知,△ABD≌△CBE,下列结论不正确的是( )
如图,已知,△ABD≌△CBE,下列结论不正确的是( )
 如图,已知,△ABD≌△CBE,下列结论不正确的是( )
如图,已知,△ABD≌△CBE,下列结论不正确的是( )| A. | ∠CBE=∠ABD | B. | BE=BD | C. | ∠CEB=∠BDE | D. | AE=ED |
16.已知⊙O的直径为8,且点P在⊙O内,则线段PO的长度( )
| A. | 小于8 | B. | 等于8 | C. | 等于4 | D. | 小于4 |
17.下列各组数中,互为相反数的是( )
| A. | 2与$\frac{1}{2}$ | B. | -(+3)与+(-3) | C. | -1与-(-1) | D. | 2与|-2| |
 如图,在平面直角坐标系xOy中,直线y=$\frac{1}{2}$x+2与x 轴交于点A,与y轴交于点C.抛物线y=ax2+bx+c的对称轴是x=-$\frac{3}{2}$且经过A、C两点,与x轴的另一交点为点B.
如图,在平面直角坐标系xOy中,直线y=$\frac{1}{2}$x+2与x 轴交于点A,与y轴交于点C.抛物线y=ax2+bx+c的对称轴是x=-$\frac{3}{2}$且经过A、C两点,与x轴的另一交点为点B.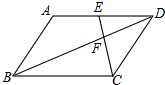 如图,在?ABCD中,点E是AD的中点,连接CE、BD交于点F,BD=12,则DF=4.
如图,在?ABCD中,点E是AD的中点,连接CE、BD交于点F,BD=12,则DF=4.