题目内容
18.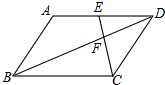 如图,在?ABCD中,点E是AD的中点,连接CE、BD交于点F,BD=12,则DF=4.
如图,在?ABCD中,点E是AD的中点,连接CE、BD交于点F,BD=12,则DF=4.
分析 先利用平行四边形的性质得AD=BC,AD∥BC,则DE=$\frac{1}{2}$BC,再利用DE∥BC可判断△DEF∽△BCF,则利用相似比可得BF=2DF,然后利用BD=DF+BF=12可计算出DF.
解答 解:∵四边形ABCD为平行四边形,
∴AD=BC,AD∥BC,
而点E是AD的中点,
∴DE=$\frac{1}{2}$BC,
∵DE∥BC,
∴△DEF∽△BCF,
∴$\frac{DF}{BF}$=$\frac{DE}{BC}$=$\frac{1}{2}$,
∴BF=2DF,
∵BD=DF+BF=12,
∴DF+2DF=12,
∴DF=4.
故答案为4.
点评 本题考查相似三角形的判定与性质:在判定两个三角形相似时,应注意利用图形中已有的公共角、公共边等隐含条件,以充分发挥基本图形的作用,寻找相似三角形的一般方法是通过作平行线构造相似三角形;在利用相似三角形的性质时主要利用相似比进行几何计算.也考查了平行四边形的性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.下列四个式子中,是方程的是( )
| A. | 3+2=5 | B. | a2+2ab+b2 | C. | 2x-3 | D. | x=1 |
9.下列实数是负数的是( )
| A. | $\sqrt{2}$ | B. | 3 | C. | 0 | D. | -1 |
6.下列各式从左到右的变形中,是因式分解的为( )
| A. | x(a-b)=ax-bx | B. | $\frac{1}{{x}^{2}}$-1=($\frac{1}{x}$+1)($\frac{1}{x}$-1) | ||
| C. | x2-1=(x+1)(x-1) | D. | x2-1+y2=(x-1)(x+1)+y2 |
13. 在△ABC中,∠A=30°,∠B=60°,则∠C=( )度.
在△ABC中,∠A=30°,∠B=60°,则∠C=( )度.
 在△ABC中,∠A=30°,∠B=60°,则∠C=( )度.
在△ABC中,∠A=30°,∠B=60°,则∠C=( )度.| A. | 70 | B. | 80 | C. | 90 | D. | 100 |
3.下列说法正确的是( )
①正整数和负整数统称为整数.
②-0.5既是分数,也是负数.
③0只表示没有.
④正数和负数统称为有理数.
⑤一个数不是正数就是负数.
⑥既不是正数也不是整数的有理数是负分数.
①正整数和负整数统称为整数.
②-0.5既是分数,也是负数.
③0只表示没有.
④正数和负数统称为有理数.
⑤一个数不是正数就是负数.
⑥既不是正数也不是整数的有理数是负分数.
| A. | ②⑥ | B. | ①②⑥ | C. | ④⑤⑥ | D. | ①⑤ |
10.三角形的内心是三角形的( )
| A. | 三条高的交点 | B. | 三条角平分线的交点 | ||
| C. | 三条中线的交点 | D. | 三条边的垂直平分线的交点 |
7.已知二次函数y=mx2+x-1的图象与x轴有两个交点,则m的取值范围是( )
| A. | m>-$\frac{1}{4}$ | B. | m≥-$\frac{1}{4}$ | C. | m>-$\frac{1}{4}$且m≠0 | D. | m≥-$\frac{1}{4}$且m≠0 |
8.下列各组中得四条线段成比例的是( )
| A. | 4cm、3cm、5cm、7cm | B. | 1cm、2cm、3cm、4cm | ||
| C. | 25cm、35cm、45cm、55cm | D. | 1cm、2cm、20cm、40cm |