Question

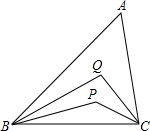如图所示，在△ABC中，∠A=60°，BP、BQ三等分∠ABC，CP、CQ三等分∠ACB．
（1）求∠BPC的度数；
（2）连结PQ，求∠BQP的度数．

Answer 1

考点：三角形内角和定理

专题：

分析：（1）由∠A=60°，根据三角形的内角和定理得，∠ABC+∠ACB=180°-60°=120°，再由线段BP、BQ把∠ABC三等分，线段CP、CQ把∠ACB三等分，得到∠PBC=

1

3

∠ABC，∠PCB=

1

3

∠ACB，于是∠PBC+∠PCB=

1

3

（∠ABC+∠ACB）=

1

3

×120°=40°，再根据三角形的内角和定理得，∠BPC=180°-40°=140°．
（2）由线段BP、BQ把∠ABC三等分，线段CP、CQ把∠ACB三等分，得到∠QBC=

2

3

∠ABC，∠QCB=

2

3

∠ACB，且P点为△QBC的内心，即PQ平分∠BPC；于是∠QBC+∠QCB=

2

3

（∠ABC+∠ACB）=

2

3

×120°=80°，再根据三角形的内角和定理得，∠BQC=180°-80°=100°，即可得到∠BQP的大小．

解答：解：（1）∵∠A=60°，
∴∠ABC+∠ACB=180°-60°=120°，
又∵线段BP、BQ把∠ABC三等分，
∴∠PBC=

1

3

∠ABC，
又∵线段CP、CE把∠ACB三等分，
∴∠PCB=

1

3

∠ACB，
∴∠PBC+∠PCB=

1

3

（∠ABC+∠ACB）=

1

3

×120°=40°，
∴∠BPC=180°-40°=140°，
（2）∵线段BP、BQ把∠ABC三等分，
∴∠QBC=

2

3

∠ABC，并且BP平分∠QBC；
又∵线段CP、CQ把∠ACB三等分，
∴QPCB=

2

3

∠ACB，并且PC平分∠QCB；
∴∠QBC+∠QCB=

2

3

（∠ABC+∠ACB）=

2

3

×120°=80°，并且P点为△QBC的内心，即QP平分∠BQC，
∴∠BQC=180°-80°=100°，
∴∠BQP=50°．

点评：本题考查了三角形的内角和定理：三角形的三个内角的和为180°．同时考查了角平分线的性质和三角形的内心性质．