题目内容
已知有理数a>0,b<0,则四个数a+b,a-b,-a+b,-a-b中最大的是 ,最小的是 .
考点:有理数大小比较
专题:
分析:利用a,b的符号,进而得出a+b,a-b,-a+b,-a-b的符号,进而得出答案.
解答:解:∵有理数a>0,b<0,
∴a+b<a,a-b>a,-a+b<b,-a-b<a
则四个数a+b,a-b,-a+b,-a-b中最大的是:a-b,最小的是:-a+b.
故答案为:a-b,-a+b.
∴a+b<a,a-b>a,-a+b<b,-a-b<a
则四个数a+b,a-b,-a+b,-a-b中最大的是:a-b,最小的是:-a+b.
故答案为:a-b,-a+b.
点评:此题主要考查了有理数比较大小,得出各项与a的关系是解题关键.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
如果代数式7a3-6a2b+5a3+ma2b的值与b无关,则( )
| A、a=0 | B、b=0 |
| C、m=0 | D、m=6 |
在下列方程中,一元二次方程的个数是( )
①3x2+7=0;②ax2+bx+c=0;③(x-2)(x+5)=x2-1;④3x2-
=0.
①3x2+7=0;②ax2+bx+c=0;③(x-2)(x+5)=x2-1;④3x2-
| 5 |
| x |
| A、1个 | B、2个 | C、3个 | D、4个 |
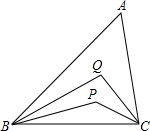 如图所示,在△ABC中,∠A=60°,BP、BQ三等分∠ABC,CP、CQ三等分∠ACB.
如图所示,在△ABC中,∠A=60°,BP、BQ三等分∠ABC,CP、CQ三等分∠ACB.