题目内容
(1)如图(1)P为⊙O上一个动点,AB=2,∠APB=30°,当P在哪个位置时,P到AB距离最大?请在图(1)中画出点P的位置和表示最大距离的线段PM,此时PM= ;
(2)如图(2),以图(1)中的AB为边,向⊙O外作等边△ABC,连接PC,求PC的最大值;
(3)如图(3)∠P=30°,等腰梯形ABCD的上底AB=2,A、B两点在∠P的两边上滑动,∠C=60°AD=4,连接DP,则DP的最小值为 .

(2)如图(2),以图(1)中的AB为边,向⊙O外作等边△ABC,连接PC,求PC的最大值;
(3)如图(3)∠P=30°,等腰梯形ABCD的上底AB=2,A、B两点在∠P的两边上滑动,∠C=60°AD=4,连接DP,则DP的最小值为

考点:圆的综合题
专题:综合题
分析:(1)当点P为优弧AB的中点时,P点到AB的距离最大,如图1,作PM⊥AB于M,根据垂径定理的推理得到PM过点O,AM=BM,再判断△OAB为等边三角形,所以OA=OB=AB=2,∠AOM=30°,则可利用含30度的直角三角形三边的关系得到AM,OM,则即可得到PM的长;
(2)当点P为优弧AB的中点时,CP最长,如图2,作PM⊥AB于M,点P′是优弧AB上异于点P的任意一点,连接OP′,利用三角形三边的关系可证明PC>P′C,
由(1)得PM=2+
,且AM=BM,再由△ABC为等边三角形得到CM⊥AB,CM=OM=
,于是可判断点M在PC上,于是利用PC=PM+MC求解;
(3)作△PAB的外接圆⊙O,如图3,连接OD交⊙O于P,此时DP的值最小,作BH⊥CD于H,OM⊥AM于M,交CD于N,由(1)可得OA=2,OM=
,AM=BM,根据等腰梯形的性质得BC=AD=4,在Rt△BCH中可计算出CH,BH,则可得到MN与BH,再计算出CN,于是得到ON=MN-OM=
,DN=CN=3,然后在Rt△DON中利用勾股定理计算出OD,然后利用DP=OD-OP求解.
(2)当点P为优弧AB的中点时,CP最长,如图2,作PM⊥AB于M,点P′是优弧AB上异于点P的任意一点,连接OP′,利用三角形三边的关系可证明PC>P′C,
由(1)得PM=2+
| 3 |
| 3 |
(3)作△PAB的外接圆⊙O,如图3,连接OD交⊙O于P,此时DP的值最小,作BH⊥CD于H,OM⊥AM于M,交CD于N,由(1)可得OA=2,OM=
| 3 |
| 3 |
解答:解:(1) 当点P为优弧AB的中点时,P点到AB的距离最大,如图1,
当点P为优弧AB的中点时,P点到AB的距离最大,如图1,
作PM⊥AB于M,
∵弧PA=弧PB,PM⊥AB,
∴PM过点O,AM=BM,
∴∠AOB=2∠APB=2×30°=60°,
∴△OAB为等边三角形,
∴OA=OB=AB=2,
∵∠AOM=
∠AOB=30°,
∴AM=
OA=1,OM=
AM=
,
∴PM=OP+PM=2+
.
故答案为2+
;
(2)当点P为优弧AB的中点时,P C最长,如图2,作PM⊥AB于M,
C最长,如图2,作PM⊥AB于M,
点P′是优弧AB上异于点P的任意一点,连接OP′,
∵OP′+OC>P′C,
而OP=OP′,
∴PC>P′C,
由(1)得PM=2+
,且AM=BM,
∵△ABC为等边三角形,
∴CM⊥AB,CM=OM=
,
∴点M在PC上,
∴PC=PM+MC=2+
+
=2+2
;
(3)作△PAB的外接圆⊙O,如图3,
 连接OD交⊙O于P,此时DP的值最小,
连接OD交⊙O于P,此时DP的值最小,
作BH⊥CD于H,OM⊥AM于M,交CD于N,
由(1)可得OA=2,OM=
,AM=BM,
∵梯形ABCD为等腰梯形,
∴BC=AD=4,
在Rt△BCH中,∠C=60°,
∴∠CBH=30°,
∴CH=
BC=2,BH=
CH=2
,
∴MN=BH=2
,CN=NH+CH=BM+CH=1+2=3,
∴ON=MN-OM=
,DN=CN=3,
在Rt△DON中,OD=
=2
,
∴DP=OD-OP=2
-2.
故答案为2
-2.
 当点P为优弧AB的中点时,P点到AB的距离最大,如图1,
当点P为优弧AB的中点时,P点到AB的距离最大,如图1,作PM⊥AB于M,
∵弧PA=弧PB,PM⊥AB,
∴PM过点O,AM=BM,
∴∠AOB=2∠APB=2×30°=60°,
∴△OAB为等边三角形,
∴OA=OB=AB=2,
∵∠AOM=
| 1 |
| 2 |
∴AM=
| 1 |
| 2 |
| 3 |
| 3 |
∴PM=OP+PM=2+
| 3 |
故答案为2+
| 3 |
(2)当点P为优弧AB的中点时,P
 C最长,如图2,作PM⊥AB于M,
C最长,如图2,作PM⊥AB于M,点P′是优弧AB上异于点P的任意一点,连接OP′,
∵OP′+OC>P′C,
而OP=OP′,
∴PC>P′C,
由(1)得PM=2+
| 3 |
∵△ABC为等边三角形,
∴CM⊥AB,CM=OM=
| 3 |
∴点M在PC上,
∴PC=PM+MC=2+
| 3 |
| 3 |
| 3 |
(3)作△PAB的外接圆⊙O,如图3,
 连接OD交⊙O于P,此时DP的值最小,
连接OD交⊙O于P,此时DP的值最小,作BH⊥CD于H,OM⊥AM于M,交CD于N,
由(1)可得OA=2,OM=
| 3 |
∵梯形ABCD为等腰梯形,
∴BC=AD=4,
在Rt△BCH中,∠C=60°,
∴∠CBH=30°,
∴CH=
| 1 |
| 2 |
| 3 |
| 3 |
∴MN=BH=2
| 3 |
∴ON=MN-OM=
| 3 |
在Rt△DON中,OD=
| ON2+DN2 |
| 3 |
∴DP=OD-OP=2
| 3 |
故答案为2
| 3 |
点评:本题考查了圆的综合题:熟练掌握垂径定理、圆周角定理、等边三角形的判定与性质和等腰梯形的性质;会根据勾股定理和含30度的直角三角形三边的关系进行几何计算.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
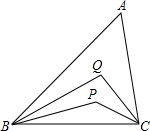 如图所示,在△ABC中,∠A=60°,BP、BQ三等分∠ABC,CP、CQ三等分∠ACB.
如图所示,在△ABC中,∠A=60°,BP、BQ三等分∠ABC,CP、CQ三等分∠ACB. 如图,四边形ABCD的对角线AC、BD相交于点O,点A、点C关于点O成中心对称,点B、点D关于点O成中心对称,且点B、D关于AC成轴对称.求证:四边形ABCD是菱形.
如图,四边形ABCD的对角线AC、BD相交于点O,点A、点C关于点O成中心对称,点B、点D关于点O成中心对称,且点B、D关于AC成轴对称.求证:四边形ABCD是菱形.