题目内容
 如图,正方形ABCD中,点P是边BC上一点,PH⊥BC交BD于点H,连接AP交BD于点E,点F为DH中点,PF交CD的延长线于点M,连接AF.
如图,正方形ABCD中,点P是边BC上一点,PH⊥BC交BD于点H,连接AP交BD于点E,点F为DH中点,PF交CD的延长线于点M,连接AF.(1)求证:△PHF≌△MDF;
(2)当点P在线段BC上运动时,∠PAF的大小是否会发生变化?若不变,请求出∠PAF的值;若变化,请说明理由;
(3)求证:BE2+DF2=EF2.
考点:四边形综合题
专题:综合题
分析:(1)根据正方形的性质得∠C=90°,而PH⊥BC,则HP∥CD,根据平行线的性质得∠FPH=∠FMD,再利用点F为DH中点得到FH=FD,然后根据“AAS”可证明△PHF≌△MDF;
(2)连接AM,如图,根据三角形全等的性质由△PHF≌△MDF得到HP=MD,FP=FM,再根据正方形的性质得AB=AD,∠CBD=45°,则可判断△BPH为等腰直角三角形,得到PB=PH,则PB=MD,于是可根据“SAS”证明△ABP≌△ADM,得到∠1=∠2,AP=AM,易得∠PAM=90°,所以△APM为等腰直角三角形,由于FM=FP,根据等腰直角三角形的性质得AF平分∠PAM,于是有∠PAF=45°;
(3)利用正方形的性质得AB=AD,∠BAD=90°,于是根据旋转的定义,把△ADF绕点A顺时针旋转90°得到△ABQ,则根据旋转的性质得∠QAF=90°,BQ=DF,AQ=AF,∠4=∠ADF,由于∠EAF=45°,则∠EAQ=45°,于是可根据“SAS”证明△AEQ≌△AEF,得到EQ=EF,由四边形ABCD为正方形得∠ADF=45°,∠3=45°,则∠4=45°,得到∠EBQ=90°,根据勾股定理得BE2+BQ2=EQ2,利用等线段代换得到BE2+DF2=EF2.
(2)连接AM,如图,根据三角形全等的性质由△PHF≌△MDF得到HP=MD,FP=FM,再根据正方形的性质得AB=AD,∠CBD=45°,则可判断△BPH为等腰直角三角形,得到PB=PH,则PB=MD,于是可根据“SAS”证明△ABP≌△ADM,得到∠1=∠2,AP=AM,易得∠PAM=90°,所以△APM为等腰直角三角形,由于FM=FP,根据等腰直角三角形的性质得AF平分∠PAM,于是有∠PAF=45°;
(3)利用正方形的性质得AB=AD,∠BAD=90°,于是根据旋转的定义,把△ADF绕点A顺时针旋转90°得到△ABQ,则根据旋转的性质得∠QAF=90°,BQ=DF,AQ=AF,∠4=∠ADF,由于∠EAF=45°,则∠EAQ=45°,于是可根据“SAS”证明△AEQ≌△AEF,得到EQ=EF,由四边形ABCD为正方形得∠ADF=45°,∠3=45°,则∠4=45°,得到∠EBQ=90°,根据勾股定理得BE2+BQ2=EQ2,利用等线段代换得到BE2+DF2=EF2.
解答:(1)证明:∵四边形ABCD为正方形,
∴∠C=90°,
∵PH⊥BC,
∴∠BPH=90°,
∴HP∥CD,
∴∠FPH=∠FMD,
∵点F为DH中点,
∴FH=FD,
在△PHF和△MDF中
,
∴△PHF≌△MDF(AAS);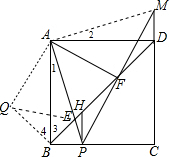
(2)∠PAF的大小不变化.
解:连接AM,如图,
∵△PHF≌△MDF,
∴HP=MD,FP=FM,
∵四边形ABCD为正方形,
∴AB=AD,∠CBD=45°,
∴△BPH为等腰直角三角形,
∴PB=PH,
∴PB=MD,
在△ABP和△ADM中
,
∴△ABP≌△ADM(SAS),
∴∠1=∠2,AP=AM,
而∠1+∠PAD=90°,
∴∠2+∠PAD=90°,即∠PAM=90°,
∴△APM为等腰直角三角形,
∵FM=FP,
∴AF平分∠PAM,
∴∠PAF=45°;
(3)证明:∵AB=AD,∠BAD=90°,
∴把△ADF绕点A顺时针旋转90°得到△ABQ,
∴∠QAF=90°,BQ=DF,AQ=AF,∠4=∠ADF,
∵∠EAF=45°,
∴∠EAQ=45°,
在△AEQ和△AEF中
,
∴△AEQ≌△AEF(SAS),
∴EQ=EF,
∵四边形ABCD为正方形,
∴∠ADF=45°,∠3=45°,
∴∠4=∠ADF=45°,
∴∠3+∠4=90°,即∠EBQ=90°,
∴BE2+BQ2=EQ2,
∴BE2+DF2=EF2.
∴∠C=90°,
∵PH⊥BC,
∴∠BPH=90°,
∴HP∥CD,
∴∠FPH=∠FMD,
∵点F为DH中点,
∴FH=FD,
在△PHF和△MDF中
|
∴△PHF≌△MDF(AAS);

(2)∠PAF的大小不变化.
解:连接AM,如图,
∵△PHF≌△MDF,
∴HP=MD,FP=FM,
∵四边形ABCD为正方形,
∴AB=AD,∠CBD=45°,
∴△BPH为等腰直角三角形,
∴PB=PH,
∴PB=MD,
在△ABP和△ADM中
|
∴△ABP≌△ADM(SAS),
∴∠1=∠2,AP=AM,
而∠1+∠PAD=90°,
∴∠2+∠PAD=90°,即∠PAM=90°,
∴△APM为等腰直角三角形,
∵FM=FP,
∴AF平分∠PAM,
∴∠PAF=45°;
(3)证明:∵AB=AD,∠BAD=90°,
∴把△ADF绕点A顺时针旋转90°得到△ABQ,
∴∠QAF=90°,BQ=DF,AQ=AF,∠4=∠ADF,
∵∠EAF=45°,
∴∠EAQ=45°,
在△AEQ和△AEF中
|
∴△AEQ≌△AEF(SAS),
∴EQ=EF,
∵四边形ABCD为正方形,
∴∠ADF=45°,∠3=45°,
∴∠4=∠ADF=45°,
∴∠3+∠4=90°,即∠EBQ=90°,
∴BE2+BQ2=EQ2,
∴BE2+DF2=EF2.
点评:本题考查了四边形的综合题:熟练掌握正方形的性质、等腰直角三角形的性质和旋转的性质;合理使用三角形全等的判定与性质;会运用勾股定理证明线段之间的关系.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

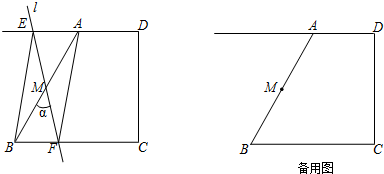
 某社区准备在甲、乙两位射箭爱好者中选出一人参加集训,两人各射了5箭,他们的总成绩(单位:环)相同,小宇根据他们的成绩绘制了如图尚不完整的统计图表,并计算了甲成绩的平均数和方差(见小宇的作业).
某社区准备在甲、乙两位射箭爱好者中选出一人参加集训,两人各射了5箭,他们的总成绩(单位:环)相同,小宇根据他们的成绩绘制了如图尚不完整的统计图表,并计算了甲成绩的平均数和方差(见小宇的作业).
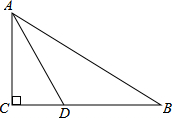 如图,在Rt△ABC中,∠B=90°,AD平分∠BAC,∠BAD=α,sinα=
如图,在Rt△ABC中,∠B=90°,AD平分∠BAC,∠BAD=α,sinα=