题目内容
16.设一元二次方程ax2+bx+c=0的两根分别为x1与x2,则:1.x1+x2=-$\frac{b}{a}$;x1x2=$\frac{c}{a}$.
2.$\frac{1}{{x}_{1}}$+$\frac{1}{{x}_{2}}$=-$\frac{b}{c}$.
3.x12+x22=$\frac{{b}^{2}-2ac}{{a}^{2}}$.
4.x12x2+x1x22=-$\frac{bc}{{a}^{2}}$.
分析 (1)由根与系数的关系,即可得出x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$;
(2)将x1+x2=-$\frac{b}{a}$、x1x2=$\frac{c}{a}$,代入$\frac{1}{{x}_{1}}$+$\frac{1}{{x}_{2}}$=$\frac{{x}_{1}+{x}_{2}}{{x}_{1}{x}_{2}}$中,即可求出结论;
(3)将x1+x2=-$\frac{b}{a}$、x1x2=$\frac{c}{a}$,代入x12+x22=(x1+x2)2-2x1x2中,即可求出结论;
(4)将x1+x2=-$\frac{b}{a}$、x1x2=$\frac{c}{a}$,代入x12x2+x1x22=x1x2•(x1+x2)中,即可求出结论.
解答 解:1、∵一元二次方程ax2+bx+c=0的两根分别为x1与x2,
∴x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$.
故答案为:-$\frac{b}{a}$;$\frac{c}{a}$.
2、∵x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$,
∴$\frac{1}{{x}_{1}}$+$\frac{1}{{x}_{2}}$=$\frac{{x}_{1}+{x}_{2}}{{x}_{1}{x}_{2}}$=-$\frac{b}{c}$.
故答案为:-$\frac{b}{c}$.
3、∵x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$,
∴x12+x22=(x1+x2)2-2x1x2=$\frac{{b}^{2}-2ac}{{a}^{2}}$.
故答案为:$\frac{{b}^{2}-2ac}{{a}^{2}}$.
4、∵x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$,
∴x12x2+x1x22=x1x2•(x1+x2)=-$\frac{bc}{{a}^{2}}$.
故答案为:-$\frac{bc}{{a}^{2}}$.
点评 本题考查了根与系数的关系,熟练掌握两根之和等于-$\frac{b}{a}$、两根之积等于$\frac{c}{a}$是解题的关键.

 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案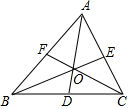 如图,D、E、F分别为△ABC各边中点,AD、BE、CF交于O点,则图中面积相等的三角形共有( )
如图,D、E、F分别为△ABC各边中点,AD、BE、CF交于O点,则图中面积相等的三角形共有( )| A. | 15对 | B. | 18对 | C. | 30对 | D. | 33对 |
| A. | 2m+3n=12 | B. | m+n=7 | C. | 2m+n=6 | D. | m+2n=6 |
 如图,将一根长24厘米的筷子,置于底面直径为6厘米,高为8厘米的圆柱形水杯中,则筷子露在杯子外面的长度至少为多少厘米?
如图,将一根长24厘米的筷子,置于底面直径为6厘米,高为8厘米的圆柱形水杯中,则筷子露在杯子外面的长度至少为多少厘米?