题目内容
9. 企业的工业废料处理有两种方式,一种是运送到垃圾厂进行集中处理,另一种是通过企业的自身设备进行处理.某企业去年每月的工业废料均为120吨,由于垃圾厂处于调试阶段,处理能力有限,该企业采取两种处理方式同时进行.
企业的工业废料处理有两种方式,一种是运送到垃圾厂进行集中处理,另一种是通过企业的自身设备进行处理.某企业去年每月的工业废料均为120吨,由于垃圾厂处于调试阶段,处理能力有限,该企业采取两种处理方式同时进行.1至6月,该企业向垃圾厂运送的工业废料y1(吨)与月份x(1≤x≤6,且x取整数)之间满足的函数关系如表:
| 月份x(月) | 1 | 2 | 3 | 4 | 5 | 6 |
| 运送的工业废料y1(吨) | 120 | 60 | 40 | 30 | 24 | 20 |
1至6月,垃圾厂处理每吨工业废料的费用z1(元) 与月份x之间满足函数关系式:z1=60x,该企业自身处理每吨工业废料的费用z2(元)与月份x之间满足函数关系式:z2=45x-5x2;7至12月,垃圾厂处理每吨工业废料的费用均为120元,该企业自身处理每吨工业废料的费用均为90元.
(1)请观察题中的表格和图象,用所学过的一次函数、反比例函数或二次函数的有关知识,分别直接写出y1、y2与x之间的函数关系式;
(2)求该企业去年哪个月用于工业废料处理的费用W(元)最多,并求出这个最多费用;
(3)今年以来,由于企业的自身设备的全面运行,该企业决定扩大产能并将所有工业废料全部自身处理,估计扩大产能后今年每月的工业废料量都将在去年每月的基础上增加 m%,同时每吨工业废料处理的费用将在去年12月份的基础上增加m%.为鼓励节能降耗,减轻企业负担,国家财政对该企业处理工业废料的费用进行了50%的补助,若该企业每月的工业废料处理费用为12150元,求m的值.
分析 (1)根据表格可知y1与x成反比例函数,从而可以得到y1与x的函数解析式;由函数图象知y2=ax2+c过点(7,19),(12,114),从而可以得到y2与x之间的函数关系式;
(2)根据题意和第(1)问中求得的函数关系可以分别表示出当1≤x≤6,且x取整数时,W与x的函数关系式和当7≤x≤12时,且x取整数时,W与x之间的函数关系式,从而可以分别求相应的最大值,从而可以得到哪个月的费用最多;
(3)根据题意可以列出关于m的方程,从而可以得到m的值.
解答 解:(1)由图表可知,y1与x成反比例函数,设${y}_{1}=\frac{k}{x}$,
∵点(1,120)在此反比例函数上,
∴$120=\frac{k}{1}$,得k=120,
∴y1=$\frac{120}{x}$(1≤x≤6,且x取整数);
∵由函数图象可知,y2=ax2+c过点(7,19),(12,114),
∴$\left\{\begin{array}{l}{a×{7}^{2}+c=19}\\{a×1{2}^{2}+c=114}\end{array}\right.$
解得,$\left\{\begin{array}{l}{a=1}\\{c=-30}\end{array}\right.$
∴y2=x2-30(7≤x≤12,且x取整数);
(2)由题意可得,
当1≤x≤6,且x取整数时:W=60x×$\frac{120}{x}$+$(45x-5{x}^{2})(120-\frac{120}{x})$=-600x2+6000x+1800=-600(x-5)2+16800,
∴当x=5时,W最大=16800(元);
当7≤x≤12时,且x取整数时,W=120×[120-(x2-30)]+90×(x2-30)=-30x2+15300,
∴当x=7时,W最大=13830(元),
∵16800>13830,
∴去年5月用于污水处理的费用最多,最多费用是16800元;
(3)由题意可得,
120(1+m%)×90×(1+m%)×(1-50%)=12150,
解得,m=50或m=-250(舍去),
即m的值是50.
点评 本题考查二次函数的应用,解题的关键是明确题意,找出所求问题需要的条件,能将二次函数化为顶点式,会求在相应的自变量x的取值范围内,函数相应的最大值,注意第(3)问中m的值是正值,不能是负值.

 华东师大版一课一练系列答案
华东师大版一课一练系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案| A. | a3•a2=a6 | B. | (a2)3=a6 | C. | (2a)(3a)=6a | D. | a6÷a2=a3 |
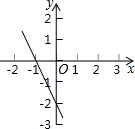 如图,是函数y=kx+b的图象,当y<-1时,x的取值范围是( )
如图,是函数y=kx+b的图象,当y<-1时,x的取值范围是( )| A. | x<-$\frac{1}{2}$ | B. | x>-$\frac{1}{2}$ | C. | x<-$\frac{1}{4}$ | D. | x>-$\frac{1}{4}$ |
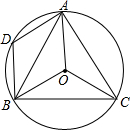 如图,在⊙0中,$\widehat{AB}$=$\widehat{AC}$,∠ACB=60°.
如图,在⊙0中,$\widehat{AB}$=$\widehat{AC}$,∠ACB=60°.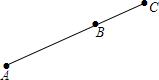 如图,A、B、C是一条公路边的三个连锁超市,且A、B、C在一条直线上,计划在A、C之间的公路边建一个配货中心P,负责向3个超市送货.
如图,A、B、C是一条公路边的三个连锁超市,且A、B、C在一条直线上,计划在A、C之间的公路边建一个配货中心P,负责向3个超市送货.