题目内容
5.已知a、b、c分别为Rt△ABC(∠C=90°)的三边的长,则关于x的一元二次方程(c+a)x2+2bx+(c-a)=0根的情况是( )| A. | 方程无实数根 | B. | 方程有两个不相等的实数根 | ||
| C. | 方程有两个相等的实数根 | D. | 无法判断 |
分析 先根据勾股定理得到a2+b2=c2,再计算出△=4b2-4(c+a)(c-a)=4(b2-c2+a2)=0,于是根据判别式的意义判断方程根的情况.
解答 解:∵a、b、c分别为Rt△ABC(∠C=90°)的三边的长,
∴a2+b2=c2,
∵△=4b2-4(c+a)(c-a)=4(b2-c2+a2),
∴△=0,
∴方程有两个相等的两个实数根.
故选C.
点评 本题考查了根的判别式:一元二次方程ax2+bx+c=0(a≠0)的根与△=b2-4ac有如下关系:当△>0时,方程有两个不相等的两个实数根;当△=0时,方程有两个相等的两个实数根;当△<0时,方程无实数根.也考查了勾股定理.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.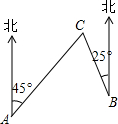 如图,C岛在A岛的北偏东45°方向,C岛在B岛的北偏西25°方向,则从C岛看A、B两岛的视角∠ACB的度数是( )
如图,C岛在A岛的北偏东45°方向,C岛在B岛的北偏西25°方向,则从C岛看A、B两岛的视角∠ACB的度数是( )
 如图,C岛在A岛的北偏东45°方向,C岛在B岛的北偏西25°方向,则从C岛看A、B两岛的视角∠ACB的度数是( )
如图,C岛在A岛的北偏东45°方向,C岛在B岛的北偏西25°方向,则从C岛看A、B两岛的视角∠ACB的度数是( )| A. | 70° | B. | 20° | C. | 35° | D. | 110° |
17.把正比例函数y=2x的图象向下平移3个单位后,所得图象的函数关系式为( )
| A. | y=2(x-3) | B. | y=2x-3 | C. | y=2x+3 | D. | y=2x |
13.下列各式从左到右的变形中,属于因式分解的是( )
| A. | (a+b)(a-b)=a2-b2 | B. | a2+2ab+b2=(a+b)2 | C. | a(a+b)=a2+ab | D. | (a-b)2=(b-a)2 |
 某住宅小区六月份1日至5日每天的用水量变化情况如图所示,则这5天该住宅小区平均每天的用水量是32吨.
某住宅小区六月份1日至5日每天的用水量变化情况如图所示,则这5天该住宅小区平均每天的用水量是32吨.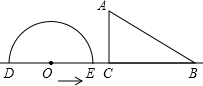 如图,形如量角器的半圆O的直径DE=12cm,形如三角形的△ABC中,∠ACB=90°,∠ABC=30°,BC=12cm,半圆O以2cm/s的速度从左向右运动,在运动过程中,点D、E始终在直线BC上,设运动时间为t(s),当t=0s时,半圆O在△ABC的左侧,OC=8cm.
如图,形如量角器的半圆O的直径DE=12cm,形如三角形的△ABC中,∠ACB=90°,∠ABC=30°,BC=12cm,半圆O以2cm/s的速度从左向右运动,在运动过程中,点D、E始终在直线BC上,设运动时间为t(s),当t=0s时,半圆O在△ABC的左侧,OC=8cm.