题目内容
2.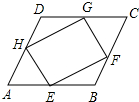 如图,在?ABCD中,E,F,G,H分别是边AB,BC,CD,DA的中点,求证:EFGH是平行四边形.
如图,在?ABCD中,E,F,G,H分别是边AB,BC,CD,DA的中点,求证:EFGH是平行四边形.
分析 首先连接BD,根据中位线的性质得出EH∥BD,EH=$\frac{1}{2}$BD,进而得出EH∥FG,EH=FG,即可得出答案.
解答  证明:连接BD,
证明:连接BD,
∵点E、F、G、H分别是边AB、BC、CD、DA的中点.
∴EH为△ABD的中位线,
∴EH∥BD,EH=$\frac{1}{2}$BD.
同理:FG∥BD,FG=$\frac{1}{2}$BD,
∴EH∥FG,EH=FG
∴四边形EFGH是平行四边形.
点评 此题主要考查了中点四边形的判定以及三角形的中位线的性质等知识,熟练掌握三角形中位线定理是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.小明在商店购买了A,B,C三种商品,恰好用去了150元,其中A,B,C三种商品的单价分别为50元、30元、10元,要求每种商品至少买一件,且A商品最多买两件,则小明的购买方案共有( )
| A. | 3种 | B. | 4种 | C. | 5种 | D. | 6种 |
17.把正比例函数y=2x的图象向下平移3个单位后,所得图象的函数关系式为( )
| A. | y=2(x-3) | B. | y=2x-3 | C. | y=2x+3 | D. | y=2x |
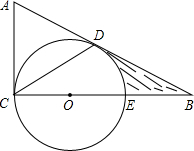 在△ABC中,∠ACB=90°,E为BC上一点,以CE为直径作⊙O,AB与⊙O相切于点D,连接CD,若BE=OE=2.
在△ABC中,∠ACB=90°,E为BC上一点,以CE为直径作⊙O,AB与⊙O相切于点D,连接CD,若BE=OE=2.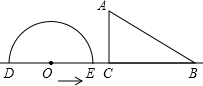 如图,形如量角器的半圆O的直径DE=12cm,形如三角形的△ABC中,∠ACB=90°,∠ABC=30°,BC=12cm,半圆O以2cm/s的速度从左向右运动,在运动过程中,点D、E始终在直线BC上,设运动时间为t(s),当t=0s时,半圆O在△ABC的左侧,OC=8cm.
如图,形如量角器的半圆O的直径DE=12cm,形如三角形的△ABC中,∠ACB=90°,∠ABC=30°,BC=12cm,半圆O以2cm/s的速度从左向右运动,在运动过程中,点D、E始终在直线BC上,设运动时间为t(s),当t=0s时,半圆O在△ABC的左侧,OC=8cm.