题目内容
1.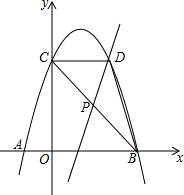 如图,已知抛物线y=ax2+bx+c(a≠0)与x轴交于A、B两点(点A在点B的左边),A(-1,0),B(3,0),与y轴交于点C(0,3)连接BC.
如图,已知抛物线y=ax2+bx+c(a≠0)与x轴交于A、B两点(点A在点B的左边),A(-1,0),B(3,0),与y轴交于点C(0,3)连接BC.(1)求抛物线的解析式;
(2)点D与点C关于抛物线对称轴对称,连接DB、DC,直线PD交直线BC于点P,且直线PD把△BCD分成面积相等的两部分,请直接写出直线PD的解析式.
分析 (1)将A(-1,0)、B(3,0)、C(0,3)三点坐标代入抛物线y=ax2+bx+c(a≠0)中,列方程组求a、b、c的值即可;
(2)根据题意可确定P点的坐标,然后根据待定系数法求得即可.
解答 解:(1)由题意,得:$\left\{\begin{array}{l}{a-b+c=0}\\{9a+3b+c=0}\\{c=3}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=-1}\\{b=2}\\{c=3}\end{array}\right.$.
故这个抛物线的解析式为y=-x2+2x+3.
(2)∵抛物线的对称轴x=-$\frac{b}{2a}$=1,点D与点C关于抛物线对称轴对称,
∴CD∥x轴,D(2,3)
∵直线PD把△BCD分成面积相等的两部分,
∴P到CD的距离等于B到CD距离的一半,
∴P是线段BC的中点,
∵B(3,0),C(0,3),
∴P($\frac{3}{2}$,$\frac{3}{2}$),
设直线PD的解析式为y=kx+b,
∴$\left\{\begin{array}{l}{\frac{3}{2}k+b=\frac{3}{2}}\\{2k+b=3}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=3}\\{b=-3}\end{array}\right.$
∴直线PD的解析式为y=3x-3.
点评 本题考查了待定系数法求二次函数和一次函数的解析式,根据已知条件求得P的坐标是解题的关键.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目



