题目内容
 如图,平面直角坐标系中,矩形OABC的顶点A、C分别在x轴和y轴的正半轴上,反比例函数y=
如图,平面直角坐标系中,矩形OABC的顶点A、C分别在x轴和y轴的正半轴上,反比例函数y=| k |
| x |
(1)求k的值;
(2)若射线OE对应的函数关系式是y=
| x |
| 6 |
(3)在(2)的条件下,连结AC,试证明:EF∥AC.
考点:反比例函数综合题,解分式方程,反比例函数系数k的几何意义,平行线的判定,勾股定理,相似三角形的判定与性质
专题:综合题
分析:(1)由△OAE面积与k的关系可求得k值.
(2)由于点E为两函数的交点,联立方程可求得点E的坐标,进而求出点B、F的坐标,由勾股定理即可求出EF的长.
(3)易证△BEF∽△BAC,从而得到∠BEF=∠BAC,进而得到两直线平行.
(2)由于点E为两函数的交点,联立方程可求得点E的坐标,进而求出点B、F的坐标,由勾股定理即可求出EF的长.
(3)易证△BEF∽△BAC,从而得到∠BEF=∠BAC,进而得到两直线平行.
解答:解:(1)连接OB,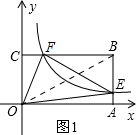 如图1所示.
如图1所示.
∵S△OAB=S△OCB,S△OCF=S△OAE=
k,
∴S△OFB=S△OBE.
∵S△OFB+S△OBE=12,
∴S△OBE=6,
∵BE=2AE,
∴S△OBE=2S△OAE=6,
∴S△OAE=
k=3.
∴k=6.
∴k的值为6.
(2)解方程
=
,得:
x=±6,
∵点E在第一象限,
∴x=6,
把x=6代入y=
,
得y=1,即点E(6,1).
∵BE=2AE,
∴点B(6,3).
把y=3代入y=
,得:
x=2.
∴点F(2,3).
∴BF=6-2=4,BE=3-1=2.
在直角△BEF中,根据勾股定理得:
EF=
=
=2
.
(3)连接AC,如图2所示.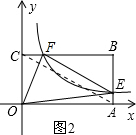
∵BF=4,BE=2,BC=6,BA=3,
∴
=
=
,
=
,
∴
=
,
∵∠B=∠B,
∴△BEF∽△BAC.
∴∠BEF=∠BAC.
∴EF∥AC.
 如图1所示.
如图1所示.∵S△OAB=S△OCB,S△OCF=S△OAE=
| 1 |
| 2 |
∴S△OFB=S△OBE.
∵S△OFB+S△OBE=12,
∴S△OBE=6,
∵BE=2AE,
∴S△OBE=2S△OAE=6,
∴S△OAE=
| 1 |
| 2 |
∴k=6.
∴k的值为6.
(2)解方程
| x |
| 6 |
| 6 |
| x |
x=±6,
∵点E在第一象限,
∴x=6,
把x=6代入y=
| 6 |
| x |
得y=1,即点E(6,1).
∵BE=2AE,
∴点B(6,3).
把y=3代入y=
| 6 |
| x |
x=2.
∴点F(2,3).
∴BF=6-2=4,BE=3-1=2.
在直角△BEF中,根据勾股定理得:
EF=
| BF2+BE2 |
=
| 42+22 |
=2
| 5 |
(3)连接AC,如图2所示.

∵BF=4,BE=2,BC=6,BA=3,
∴
| BF |
| BC |
| 4 |
| 6 |
| 2 |
| 3 |
| BE |
| BA |
| 2 |
| 3 |
∴
| BF |
| BC |
| BE |
| BA |
∵∠B=∠B,
∴△BEF∽△BAC.
∴∠BEF=∠BAC.
∴EF∥AC.
点评:本题考查了反比例函数的比例系数k的几何意义、相似三角形的判定与性质、勾股定理、平行线的判定等知识,有一定的综合性.

练习册系列答案
相关题目
 某商场为了吸引顾客,设立了可以自由转动的转盘(如图,转盘被均匀分为20份),并规定:顾客每购买200元的商品,就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准红色、黄色、绿色区域,那么顾客就可以分别获得200元、100元、50元的购物券,凭购物券可以在该商场继续购物.如果顾客不愿意转转盘,那么可以直接获得购物券30元.
某商场为了吸引顾客,设立了可以自由转动的转盘(如图,转盘被均匀分为20份),并规定:顾客每购买200元的商品,就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准红色、黄色、绿色区域,那么顾客就可以分别获得200元、100元、50元的购物券,凭购物券可以在该商场继续购物.如果顾客不愿意转转盘,那么可以直接获得购物券30元.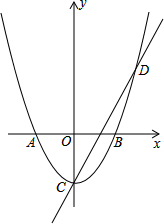 如图,在平面直角坐标系中,抛物线与x轴交于点A(-1,0)和点B(1,0),直线y=2x-1与y轴交于点C,与抛物线交于点C、D.
如图,在平面直角坐标系中,抛物线与x轴交于点A(-1,0)和点B(1,0),直线y=2x-1与y轴交于点C,与抛物线交于点C、D.