题目内容
1. 为解决停车难的问题,在如图一段长56米的路段开辟停车位,每个车位是长5米、宽2.2米的矩形,矩形的边与路的边缘成45°角,那么这个路段最多可以划出17个这样的停车位($\sqrt{2}$≈1.4)
为解决停车难的问题,在如图一段长56米的路段开辟停车位,每个车位是长5米、宽2.2米的矩形,矩形的边与路的边缘成45°角,那么这个路段最多可以划出17个这样的停车位($\sqrt{2}$≈1.4)
分析 如图,根据三角函数可求BC,CE,设至多可划x个车位,依题意可列不等式2.2×$\sqrt{2}$x+(5-2.2)×$\frac{\sqrt{2}}{2}$≤56,解不等式即可求解.
解答  解:如图,CE=2.2÷sin45°=2.2×$\sqrt{2}$,BC=(5-2.2)×sin45°=(5-2.2)×$\frac{\sqrt{2}}{2}$,
解:如图,CE=2.2÷sin45°=2.2×$\sqrt{2}$,BC=(5-2.2)×sin45°=(5-2.2)×$\frac{\sqrt{2}}{2}$,
设至多可划x个车位,依题意可列不等式
2.2×$\sqrt{2}$x+(5-2.2)×$\frac{\sqrt{2}}{2}$≤56,
将$\sqrt{2}$=1.4代入不等式,化简整理得,11x≤193,
解得x$≤17\frac{6}{11}$,因为是正整数,所以x=17,
所以这个路段最多可以划出17个这样的停车位.
故答案为17.
点评 考查了解直角三角形的应用,主要是三角函数及运算,关键把实际问题转化为数学问题加以计算.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.已知点A(x1,y1)和点B(x2,y2)是直线y=2x+3上的两个点,如果x1<x2,那么y1与y2的大小关系正确的是 ( )
| A. | y1>y2 | B. | y1<y2 | C. | y1=y2 | D. | 无法判断 |
16.下列说法中正确的是( )
| A. | 两条对角线垂直的四边形的菱形 | |
| B. | 对角线垂直且相等的四边形是正方形 | |
| C. | 两条对角线相等的四边形是矩形 | |
| D. | 两条对角线相等的平行四边形是矩形 |
6.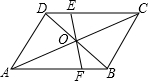 如图,?ABCD中,EF过对角线的交点O分别与CD、AB交于点E、F,AB=4,AD=3,OF=1.3,则四边形BCEF的周长为( )
如图,?ABCD中,EF过对角线的交点O分别与CD、AB交于点E、F,AB=4,AD=3,OF=1.3,则四边形BCEF的周长为( )
 如图,?ABCD中,EF过对角线的交点O分别与CD、AB交于点E、F,AB=4,AD=3,OF=1.3,则四边形BCEF的周长为( )
如图,?ABCD中,EF过对角线的交点O分别与CD、AB交于点E、F,AB=4,AD=3,OF=1.3,则四边形BCEF的周长为( )| A. | 8.3 | B. | 9.6 | C. | 12.6 | D. | 13.6 |
13.若x轴上的点P到y轴的距离为3,则点P的坐标为( )
| A. | (0,3) | B. | (0,3)或(0,-3) | C. | (3,0) | D. | (3,0)或(-3,0) |
11.据报道,中国内地首次采用“全无人驾驶”的燕房线地铁有望年底完工,列车通车后将极大改善房山和燕山居民的出行条件,预计年输送乘客可达7300万人次,将7300用科学记数法表示应为( )
| A. | 73×102 | B. | 7.3×103 | C. | 0.73×104 | D. | 7.3×102 |