题目内容
15.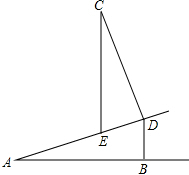 如图,AD是一段斜坡,AB是水平线,现为了测斜坡上一点D的铅直高度(即垂线段DB的长度),小亮在D处立上一竹竿CD,并保证CD=AB,CD⊥AD,然后在竿顶C处垂下一根细绳.(细绳末端挂一重锤,以使细绳与水平线垂直).细绳与斜坡AD交于点E,此时他测得DE=2米,求DB的长度.
如图,AD是一段斜坡,AB是水平线,现为了测斜坡上一点D的铅直高度(即垂线段DB的长度),小亮在D处立上一竹竿CD,并保证CD=AB,CD⊥AD,然后在竿顶C处垂下一根细绳.(细绳末端挂一重锤,以使细绳与水平线垂直).细绳与斜坡AD交于点E,此时他测得DE=2米,求DB的长度.
分析 延长CE交AB于F,根据等角的余角相等求出∠A=∠C,再利用“角边角”证明△ABD和△CDE全等,根据全等三角形对应边相等可得DB=DE.
解答 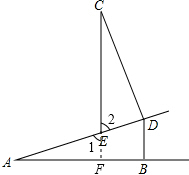 解:如图,延长CE交AB于F,
解:如图,延长CE交AB于F,
则∠A+∠1=90°,∠C+∠2=90°,
∵∠1=∠2(对顶角相等),
∴∠A=∠C,
在△ABD和△CDE中,
$\left\{\begin{array}{l}{∠A=∠C}\\{∠ABD=∠CDE=90°}\\{AB=CD}\end{array}\right.$,
∴△ABD≌△CDE(ASA),
∴DB=DE,
∵DE=2米,
∴DB的长度是2米.
点评 本题考查了全等三角形的应用,仔细观察图形求出∠A=∠C是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.将分式$\frac{xy}{x+y}$中的x,y的值同时扩大10倍,则分式的值( )
| A. | 扩大100倍 | B. | 扩大10倍 | C. | 不变 | D. | 缩小为原来的$\frac{1}{10}$ |
4.下列因式分解完全正确的是( )
| A. | -2a2+4a=-2a(a+2) | B. | -4x2-y2=-(2x+y)2 | ||
| C. | a2-8ab+16b2=(a+4b)2 | D. | 2x2+xy-y2=(2x-y)(x+y) |
 已知点O(0,0),B(2,3),点A在坐标轴上,且S△AOB=6.
已知点O(0,0),B(2,3),点A在坐标轴上,且S△AOB=6.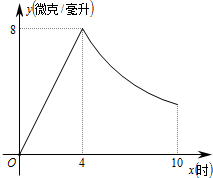 某药品研究所开发一种抗菌新药,经多年动物实验,首次用于临床人体实验.测得成人服药后血液中药物浓度y(微克/毫升)与服药时间x小时之间的函数关系如图所示(当4≤x≤10时,y与x成反比).
某药品研究所开发一种抗菌新药,经多年动物实验,首次用于临床人体实验.测得成人服药后血液中药物浓度y(微克/毫升)与服药时间x小时之间的函数关系如图所示(当4≤x≤10时,y与x成反比).