题目内容
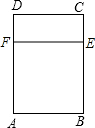 现有铝合金窗框材料8米,准备用它做一个如图所示的长方形窗架(窗架宽度AB必须小于窗架的高度BC).已知窗台距离房屋天花板2.2米.设AB为x米,窗架的总面积为S平方米.试写出S与x的函数关系式,并求自变量x的取值范围.
现有铝合金窗框材料8米,准备用它做一个如图所示的长方形窗架(窗架宽度AB必须小于窗架的高度BC).已知窗台距离房屋天花板2.2米.设AB为x米,窗架的总面积为S平方米.试写出S与x的函数关系式,并求自变量x的取值范围.考点:根据实际问题列二次函数关系式
专题:
分析:求矩形面积问题,先要求出矩形的宽x,长
,用矩形面积公式表达函数关系式,再结合已知求出自变量x的取值范围.
| 8-3x |
| 2 |
解答:解:设窗架的宽AB为x米,长为
米,
则窗户的总面积S=x•
=-
x2+4x,
∵窗架宽度AB必须小于窗架的高度BC,
∴x<
,
解得:x<
,
∵窗台距离房屋天花板2.2米,
∴
<2.2,
解得:x>1.2,
∴自变量x的取值范围1.2<x<
.
答:S与x的函数关系式为S=-
x2+4x.(1.2<x<
)
| 8-3x |
| 2 |
则窗户的总面积S=x•
| 8-3x |
| 2 |
| 3 |
| 2 |
∵窗架宽度AB必须小于窗架的高度BC,
∴x<
| 8-3x |
| 2 |
解得:x<
| 8 |
| 5 |
∵窗台距离房屋天花板2.2米,
∴
| 8-3x |
| 2 |
解得:x>1.2,
∴自变量x的取值范围1.2<x<
| 8 |
| 5 |
答:S与x的函数关系式为S=-
| 3 |
| 2 |
| 8 |
| 5 |
点评:本题考查用面积法求二次函数解析式及二次函数的实际应用.此题为数学建模题,借助二次函数解决实际问题.

练习册系列答案
相关题目
 如图,在Rt△ABC中,∠C=90°,BC=4,AC=3,以CD为直径的⊙O与AB相切于E,求⊙O的半径.
如图,在Rt△ABC中,∠C=90°,BC=4,AC=3,以CD为直径的⊙O与AB相切于E,求⊙O的半径. 如图,已知AB是⊙O的直径,PA切⊙O于点A,OP交⊙O于点C,连接BC,且BC=2
如图,已知AB是⊙O的直径,PA切⊙O于点A,OP交⊙O于点C,连接BC,且BC=2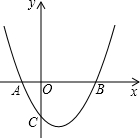 如图,抛物线y=x2-2x-3与x轴交于A、B两点,与y轴交于点C.
如图,抛物线y=x2-2x-3与x轴交于A、B两点,与y轴交于点C.