题目内容
已知抛物线的顶点坐标为(-1.-2),并且与y轴交于点(0,-3),求这条抛物线的解析式.
考点:待定系数法求二次函数解析式
专题:
分析:由于已知抛物线的顶点坐标,则设抛物线的顶点式为y=a(x+1)2-2(a≠0),再把(0,-3)代入可计算出a的值,然后把抛物线的解析式化为一般式即可.
解答:解:由题意,抛物线的顶点坐标为(-1,-2)
设抛物线的解析式为y=a(x+1)2-2(a≠0),
把(0,-3)代入上式得:a-2=-3,
解得,a=-1.
所以,这条抛物线的解析式为:y=-(x+1)2-2.
设抛物线的解析式为y=a(x+1)2-2(a≠0),
把(0,-3)代入上式得:a-2=-3,
解得,a=-1.
所以,这条抛物线的解析式为:y=-(x+1)2-2.
点评:本题考查了待定系数法法求二次函数解析式:先设二次函数的解析式(一般式、顶点式或交点式),然后把二次函数上的点的坐标代入得到方程组,再解方程组,从而确定二次函数的解析式.

练习册系列答案
相关题目

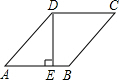 如图,在菱形ABCD中,DE⊥AB于E,DE=8,sinA=
如图,在菱形ABCD中,DE⊥AB于E,DE=8,sinA= 如图,有一块直角三角形纸片沿直线AD折叠,使AC落在斜边AB上,且点C与点E重合.已知两直角边AC=6cm,BC=8cm,求CD的长.
如图,有一块直角三角形纸片沿直线AD折叠,使AC落在斜边AB上,且点C与点E重合.已知两直角边AC=6cm,BC=8cm,求CD的长.
 如图,点B在线段AC上,点E在线段BD上,∠ABD=∠DBC,AB=DB,EB=CB,M、N分别是AE、CD的中点,判断BM与BN的关系,并说明理由.
如图,点B在线段AC上,点E在线段BD上,∠ABD=∠DBC,AB=DB,EB=CB,M、N分别是AE、CD的中点,判断BM与BN的关系,并说明理由.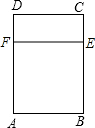 现有铝合金窗框材料8米,准备用它做一个如图所示的长方形窗架(窗架宽度AB必须小于窗架的高度BC).已知窗台距离房屋天花板2.2米.设AB为x米,窗架的总面积为S平方米.试写出S与x的函数关系式,并求自变量x的取值范围.
现有铝合金窗框材料8米,准备用它做一个如图所示的长方形窗架(窗架宽度AB必须小于窗架的高度BC).已知窗台距离房屋天花板2.2米.设AB为x米,窗架的总面积为S平方米.试写出S与x的函数关系式,并求自变量x的取值范围.