题目内容
11.在等腰△ABC中,AB=AC=13,BC=10,求sinB,cosB.分析 过A作BC边上的垂线,根据三线合一性质,就可以求出AD的长,在直角△ABD中,利用三角函数定义求解.
解答  解:作AD⊥BC与D,
解:作AD⊥BC与D,
∵AB=AC=13,D是BC的中点,即BD=5,
∴AD=$\sqrt{A{B}^{2}-B{D}^{2}}$=12,
∴sinB=$\frac{AD}{AB}$=$\frac{12}{13}$,
cosB=$\frac{BD}{AB}$=$\frac{5}{13}$.
点评 本题考查锐角三角函数的定义:在直角三角形中,锐角的正弦为对边比斜边,余弦为邻边比斜边,正切为对边比邻边.

练习册系列答案
相关题目
1.用配方法将方程x2+4x-96=0变形,结果为( )
| A. | (x+2)2=100 | B. | (x-2)2=92 | C. | (x+2)2=-100 | D. | (x-2)2=-100 |
2.已知整式x2y的值是2,则5x2y+5xy-7x-(4x2y+5xy-7x)的值是( )
| A. | $\frac{1}{2}$ | B. | -2 | C. | 2 | D. | 4 |
20.$\sqrt{64}$的平方根为( )
| A. | 8 | B. | -8 | C. | $2\sqrt{2}$ | D. | $±2\sqrt{2}$ |
 如图,在面积为2a的正方形ABCD中,截得直角三角形ABE的而积为$\frac{\sqrt{3}}{3}$a,求BE的长.
如图,在面积为2a的正方形ABCD中,截得直角三角形ABE的而积为$\frac{\sqrt{3}}{3}$a,求BE的长.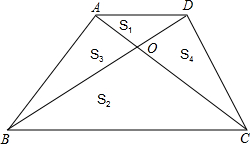 如图,梯形ABCD中,AD平行于BC,对角线AC,BD相交于点O;4个小三角形的面积是S1、S2、S3、S4.
如图,梯形ABCD中,AD平行于BC,对角线AC,BD相交于点O;4个小三角形的面积是S1、S2、S3、S4.