题目内容
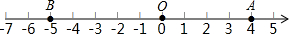 已知数轴上点A,B,C所表示的数分别是4,-5,x.
已知数轴上点A,B,C所表示的数分别是4,-5,x.(1)求线段AB的长.
(2)若A、B、C三点中有一点是其它两点的中点,求x的值.
(3)若点C在原点,此时A、C、B三点分别以每秒1个单位、2个单位、4个单位向数轴的正方向运动,当A、B、C三点中有一点是其它两点的中点时,求运动的时间.
考点:一元一次方程的应用,数轴,两点间的距离
专题:几何动点问题
分析:(1)线段AB的长等于A点表示的数减去B点表示的数;
(2)分三种情况:C为AB的中点;B为AC的中点;A为BC的中点;利用数轴上求线段长度的方法列出方程求得答案即可;
(3)设运动时间为t,分三种情况:C为AB的中点;B为AC的中点;A为BC的中点;利用数轴上求线段长度的方法列出方程求得答案即可.
(2)分三种情况:C为AB的中点;B为AC的中点;A为BC的中点;利用数轴上求线段长度的方法列出方程求得答案即可;
(3)设运动时间为t,分三种情况:C为AB的中点;B为AC的中点;A为BC的中点;利用数轴上求线段长度的方法列出方程求得答案即可.
解答:解:(1)AB=4-(-5)=9;
(2)①当C为AB的中点,
则4-x=x-(-5),
解得:x=-
;
②当B为AC的中点,
则4-(-5)=-5-x
解得:x=-14;
③当A为BC的中点,
则x-4=4-(-5)
解得:x=13;
(3)设运动时间为t秒,
①当C为AB的中点,
则4+t-2t=2t-(-5+4t),
解得:t=1;
②当B为AC的中点,
则4+t-(-5+4t)=-5+4t-2t
解得:t=
;
③当A为BC的中点,
则-5+4t-(4+t)=4+t-2t
x-4=4-(-5)
解得:t=
.
综上所知,当运动时间为1秒、
秒、
秒时,A、B、C三点中有一点是其它两点的中点.
(2)①当C为AB的中点,
则4-x=x-(-5),
解得:x=-
| 1 |
| 2 |
②当B为AC的中点,
则4-(-5)=-5-x
解得:x=-14;
③当A为BC的中点,
则x-4=4-(-5)
解得:x=13;
(3)设运动时间为t秒,
①当C为AB的中点,
则4+t-2t=2t-(-5+4t),
解得:t=1;
②当B为AC的中点,
则4+t-(-5+4t)=-5+4t-2t
解得:t=
| 14 |
| 5 |
③当A为BC的中点,
则-5+4t-(4+t)=4+t-2t
x-4=4-(-5)
解得:t=
| 13 |
| 4 |
综上所知,当运动时间为1秒、
| 14 |
| 5 |
| 13 |
| 4 |
点评:此题考查一元一次方程的实际运用,利用数轴上求线段长度的方法,找出等量关系,解决问题.

练习册系列答案
相关题目
在-
,-|-6|,-(-5),-32,(-1)2,-20,0中非正数有( )
| 2 |
| 3 |
| A、2个 | B、3个 | C、4个 | D、5个 |
用旗子摆出如图一组三角形图案,按此规律推断,当三角形每边上有n枚棋子时,该三角形的棋子总数S等于( )


| A、3n-2 | B、3n-3 |
| C、2n-2 | D、2n-3 |


 如图,在Rt△ABC中,∠ACB=90°,△DCE是△ABC绕着点C顺时针方向旋转得到的,此时B、C、E在同一直线上.求:
如图,在Rt△ABC中,∠ACB=90°,△DCE是△ABC绕着点C顺时针方向旋转得到的,此时B、C、E在同一直线上.求: 如图,△ABC内接于⊙O.
如图,△ABC内接于⊙O.