题目内容
用旗子摆出如图一组三角形图案,按此规律推断,当三角形每边上有n枚棋子时,该三角形的棋子总数S等于( )


| A、3n-2 | B、3n-3 |
| C、2n-2 | D、2n-3 |
考点:规律型:图形的变化类
专题:
分析:由题意可知:用每一条边上的棋子数乘以边数3,再减去三角形顶点处公共棋子,列式整理即可得解.
解答:解:n=2时,s=3×2-3=3,
n=3时,s=3×3-3=6,
n=4时,s=3×4-3=9,
n=5时,s=3×5-3=12,
…,
依此类推,三角形的边上有n枚棋子时,s=3n-3.
故选:B.
n=3时,s=3×3-3=6,
n=4时,s=3×4-3=9,
n=5时,s=3×5-3=12,
…,
依此类推,三角形的边上有n枚棋子时,s=3n-3.
故选:B.
点评:此题考查图形的变化规律,关键在于观察出三角形顶点处的棋子被两边公用,重复计算了一次.

练习册系列答案
相关题目
下列四个命题中,真命题是( )
| A、两条直线被第三条直线所截,内错角相等 |
| B、如果∠1和∠2是对顶角,那么∠1=∠2 |
| C、三角形的一个外角大于任何一个内角 |
| D、如果a≠b,b≠c,那么a≠c |
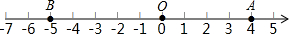 已知数轴上点A,B,C所表示的数分别是4,-5,x.
已知数轴上点A,B,C所表示的数分别是4,-5,x. 如图,∠BAD=∠CAE=90°,AB=AD,AE=AC,AF⊥CF,垂足为F.
如图,∠BAD=∠CAE=90°,AB=AD,AE=AC,AF⊥CF,垂足为F. 已知:如图,∠A=∠D=90°,AB=DC,AC、BD相交于点E.求证:
已知:如图,∠A=∠D=90°,AB=DC,AC、BD相交于点E.求证: 如图,在Rt△ABC中,∠C=90°,点E在斜边AB上,以AE为直径的⊙O与BC相切于点D,若BE=6,BD=6
如图,在Rt△ABC中,∠C=90°,点E在斜边AB上,以AE为直径的⊙O与BC相切于点D,若BE=6,BD=6