题目内容
2.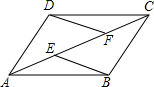 如图,E,F是平行四边形ABCD的对角线AC上的两点,AE=CF,求证:DF=BE.
如图,E,F是平行四边形ABCD的对角线AC上的两点,AE=CF,求证:DF=BE.
分析 由平行四边形的性质得出DC∥AB,DC=AB,由平行线的性质得出∠DCA=∠BAC,由SAS证明△ABE≌△CDF,即可得出结论.
解答 证明:在平行四边形ABCD中,DC∥AB,DC=AB,
∴∠DCA=∠BAC,
在△DCF和△BAE中,$\left\{\begin{array}{l}DC=BA\\∠DCA=∠BAC\\ CF=AE\end{array}\right.$,
∴△DCF≌△BAE(SAS),
∴DF=BE.
点评 本题主要考查了平行四边形的性质及全等三角形的判定及性质,熟练掌握平行四边形的性质,证明三角形全等是解决问题的关键.

练习册系列答案
相关题目
15.某班学生积极参加献爱心活动,该班50名学生的捐款统计情况如下表:
则他们捐款金额的中位数和平均数分别是( )
| 金额/元 | 5 | 10 | 20 | 50 | 100 |
| 人数 | 4 | 16 | 15 | 9 | 6 |
| A. | 10,20.6 | B. | 20,20.6 | C. | 10,30.6 | D. | 20,30.6 |
17.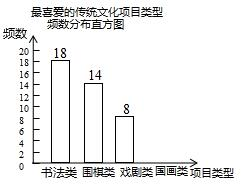 某校为更好地培养学生兴趣,开展“拓展课程走班选课”活动,随机抽查了部分学生,了解他们最喜爱的项目类型(分为书法、围棋、戏剧、国画共4类),并将统计结果绘制成如图不完整的频数分布表及频数分布直方图.
某校为更好地培养学生兴趣,开展“拓展课程走班选课”活动,随机抽查了部分学生,了解他们最喜爱的项目类型(分为书法、围棋、戏剧、国画共4类),并将统计结果绘制成如图不完整的频数分布表及频数分布直方图.
最喜爱的传统文化项目类型频数分布表
根据以上信息完成下列问题:
(1)频数分布表中a=0.36,b=10;
(2)补全频数分布直方图;
(3)若全校共有学生1500名,估计该校最喜爱围棋的学生大约有多少人?
 某校为更好地培养学生兴趣,开展“拓展课程走班选课”活动,随机抽查了部分学生,了解他们最喜爱的项目类型(分为书法、围棋、戏剧、国画共4类),并将统计结果绘制成如图不完整的频数分布表及频数分布直方图.
某校为更好地培养学生兴趣,开展“拓展课程走班选课”活动,随机抽查了部分学生,了解他们最喜爱的项目类型(分为书法、围棋、戏剧、国画共4类),并将统计结果绘制成如图不完整的频数分布表及频数分布直方图.最喜爱的传统文化项目类型频数分布表
| 项目类型 | 频数 | 频率 |
| 书法类 | 18 | a |
| 围棋类 | 14 | 0.28 |
| 喜剧类 | 8 | 0.16 |
| 国画类 | b | 0.20 |
(1)频数分布表中a=0.36,b=10;
(2)补全频数分布直方图;
(3)若全校共有学生1500名,估计该校最喜爱围棋的学生大约有多少人?
12.如图1~3,在直角边分别为3和4的直角三角形中,每多作一条斜边上的高就增加一个三角形的内切圆,依此类推,图6中有6个直角三角形的内切圆,它们的面积分别记为S1,S2,S3,…,S6,则S1+S2+S3+…+S6的值是( )


| A. | π | B. | $\sqrt{2}$π | C. | 1.6π | D. | $\frac{3}{2}$π |
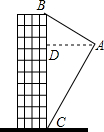 如图,航拍无人机从点A处测得一幢建筑物顶部B的仰角为32°,测得底部C的仰角为62°,此时航拍无人机与该建筑物的水平距离AD为54米,求该建筑物的高度BC(精确到0.1米,参考数据:sin 32°=0.530,cos32°=0.848,tan32°=0.625,sin 62°=0.883,cos62°=0.469,tan62°=1.88)
如图,航拍无人机从点A处测得一幢建筑物顶部B的仰角为32°,测得底部C的仰角为62°,此时航拍无人机与该建筑物的水平距离AD为54米,求该建筑物的高度BC(精确到0.1米,参考数据:sin 32°=0.530,cos32°=0.848,tan32°=0.625,sin 62°=0.883,cos62°=0.469,tan62°=1.88)