Question

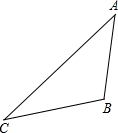如图，游客从某旅游区的景点A处下山至C处有两种路径．一种是从A沿直线步行到C；另一种是先从A沿索道乘缆车到B，然后从B沿直线步行到C．现有甲、乙两位游客从A处下山，甲沿AC匀速步行，速度为45m/min．在甲出发2min后，乙开始从A乘缆车到B，在B处停留5min后，再从B匀速步行到C，二人同时到达．已知缆车匀速直线运动的速度为180m/min，山路AC长为2430m，且测得∠CBA=45°，∠CBA=105°．（参考数据：

2

≈1.4，

3

≈1.7）．
（1）求索道AB的长；
（2）求乙的步行速度．

Answer 1

考点：解直角三角形的应用

专题：

分析：（1）如图，过B点作BD垂直于AC，垂足为D点．通过解Rt△BDC得到CD=

3

x，则由CD+AD=AC求得x=900，所以AB=

2

x=900

2

=1260m；
（2）分别求得甲沿AC匀速步行到C所用时间、乙从A乘缆车到B所用时间，则易求乙从B匀速步行到C所用的时间为，故乙的步行速度为

BC

40

=

1800

40

=45m/min．

解答：解：（1）过B点作BD垂直于AC，垂足为D点，
设BD=xm，则AD=xm，
在Rt△BDC中，tan∠BCA=

BD

CD

，
即tan30°=

x

CD

，
∴CD=

3

x，
∵CD+AD=AC，
∴

3

x+x=2430，
解得x=900，
所以AB=

2

x=900

2

=1260m．

（2）甲沿AC匀速步行到C所用时间为

2430

45

，
乙从A乘缆车到B所用时间为

1260

180

，
∴乙从B匀速步行到C所用的时间为54-2-7-5=40min，
∴乙的步行速度为

BC

40

=

1800

40

=45m/min．

点评：考查了解直角三角形的应用，本题给出实际应用问题，求索道的长并研究甲、乙二人到达时间的问题．着重考查了同角三角函数的基本关系、正余弦定理解三角形和解三角形的实际应用等知识，属于中档题．