题目内容
 如图,圆柱的高为8cm,底面直径4cm,在圆柱下底面的A点有一只蚂蚁,它想吃到上底面上与A点相对的B点处的食物,它需要爬行的最短路程是多少厘米?(π≈3)
如图,圆柱的高为8cm,底面直径4cm,在圆柱下底面的A点有一只蚂蚁,它想吃到上底面上与A点相对的B点处的食物,它需要爬行的最短路程是多少厘米?(π≈3)考点:平面展开-最短路径问题
专题:
分析:首先将此圆柱展成平面图,根据两点间线段最短,可得AB最短,由勾股定理即可求得需要爬行的最短路程.
解答: 解:将此圆柱展成平面图得:
解:将此圆柱展成平面图得:
∵有一圆柱,它的高等于8cm,底面直径等于4cm(π≈3),
∴AC=8cm,BC=
BB′=
×4π=6(cm),
∴AB=
=10(cm).
答:它需要爬行的最短路程为10cm.
 解:将此圆柱展成平面图得:
解:将此圆柱展成平面图得:∵有一圆柱,它的高等于8cm,底面直径等于4cm(π≈3),
∴AC=8cm,BC=
| 1 |
| 2 |
| 1 |
| 2 |
∴AB=
| AC2+BC2 |
答:它需要爬行的最短路程为10cm.
点评:此题主要考查了平面展开图求最短路径问题,将圆柱体展开,根据两点之间线段最短,运用勾股定理解答是解题关键.

练习册系列答案
相关题目
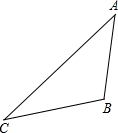 如图,游客从某旅游区的景点A处下山至C处有两种路径.一种是从A沿直线步行到C;另一种是先从A沿索道乘缆车到B,然后从B沿直线步行到C.现有甲、乙两位游客从A处下山,甲沿AC匀速步行,速度为45m/min.在甲出发2min后,乙开始从A乘缆车到B,在B处停留5min后,再从B匀速步行到C,二人同时到达.已知缆车匀速直线运动的速度为180m/min,山路AC长为2430m,且测得∠CBA=45°,∠CBA=105°.(参考数据:
如图,游客从某旅游区的景点A处下山至C处有两种路径.一种是从A沿直线步行到C;另一种是先从A沿索道乘缆车到B,然后从B沿直线步行到C.现有甲、乙两位游客从A处下山,甲沿AC匀速步行,速度为45m/min.在甲出发2min后,乙开始从A乘缆车到B,在B处停留5min后,再从B匀速步行到C,二人同时到达.已知缆车匀速直线运动的速度为180m/min,山路AC长为2430m,且测得∠CBA=45°,∠CBA=105°.(参考数据:
 在平面直角坐标系中,已知点A(3,0)、B(3,4)是以AB为边的正方形ABCD的两个顶点,如图所示.
在平面直角坐标系中,已知点A(3,0)、B(3,4)是以AB为边的正方形ABCD的两个顶点,如图所示. 已知:如图,在△ABC中,AB=AC,∠A=30°,线段AB的垂直平分线交AB于点D,交AC于点,连接BE,则∠CBE=
已知:如图,在△ABC中,AB=AC,∠A=30°,线段AB的垂直平分线交AB于点D,交AC于点,连接BE,则∠CBE=