题目内容
 △ABC中,∠ACB=90°,以AB、AC为边向外作正方形ABEF和正方形ACDG,试探究△AGF的面积与△ABC的面积有怎样的数量关系,并证明你的结论.
△ABC中,∠ACB=90°,以AB、AC为边向外作正方形ABEF和正方形ACDG,试探究△AGF的面积与△ABC的面积有怎样的数量关系,并证明你的结论.考点:全等三角形的判定与性质,正方形的性质
专题:
分析:△AGF的面积=△ABC的面积,过F作FH⊥GA交AG的延长线于H,根据正方形的性质和已知条件可证明△ACB≌△AHF,所以HF=BC,再根据等底等高的三角形面积相等即可得问题结论.
解答:解:△AGF的面积=△ABC的面积,
 理由如下:∵四边形ABEF和四边形ACDG是正方形,
理由如下:∵四边形ABEF和四边形ACDG是正方形,
∴AG=AC,AB=AF,∠ACB=∠BAF=90°,
∴∠CAB+∠BAH=∠BAH∠HAF=0=90°,
∴∠CAB=∠FAH,
在△ACB和△AHF中,
,
∴△ACB≌△AHF,
∴BC=HF,
∵S△AGF=
AG•HF,S△ACB=
AC•BC,
∴△AGF的面积=△ABC的面积.
 理由如下:∵四边形ABEF和四边形ACDG是正方形,
理由如下:∵四边形ABEF和四边形ACDG是正方形,∴AG=AC,AB=AF,∠ACB=∠BAF=90°,
∴∠CAB+∠BAH=∠BAH∠HAF=0=90°,
∴∠CAB=∠FAH,
在△ACB和△AHF中,
|
∴△ACB≌△AHF,
∴BC=HF,
∵S△AGF=
| 1 |
| 2 |
| 1 |
| 2 |
∴△AGF的面积=△ABC的面积.
点评:本题考查了正方形的性质、全等三角形的判定和性质以及三角形面积公式的运用,解题的根据是正确添加辅助线构造全等三角形进而得到BC=HF.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,两个平行四边形的面积分别为18、12,两阴影部分的面积分别为a、b(a>b),则(a-b)等于( )
如图,两个平行四边形的面积分别为18、12,两阴影部分的面积分别为a、b(a>b),则(a-b)等于( )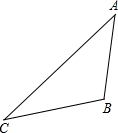 如图,游客从某旅游区的景点A处下山至C处有两种路径.一种是从A沿直线步行到C;另一种是先从A沿索道乘缆车到B,然后从B沿直线步行到C.现有甲、乙两位游客从A处下山,甲沿AC匀速步行,速度为45m/min.在甲出发2min后,乙开始从A乘缆车到B,在B处停留5min后,再从B匀速步行到C,二人同时到达.已知缆车匀速直线运动的速度为180m/min,山路AC长为2430m,且测得∠CBA=45°,∠CBA=105°.(参考数据:
如图,游客从某旅游区的景点A处下山至C处有两种路径.一种是从A沿直线步行到C;另一种是先从A沿索道乘缆车到B,然后从B沿直线步行到C.现有甲、乙两位游客从A处下山,甲沿AC匀速步行,速度为45m/min.在甲出发2min后,乙开始从A乘缆车到B,在B处停留5min后,再从B匀速步行到C,二人同时到达.已知缆车匀速直线运动的速度为180m/min,山路AC长为2430m,且测得∠CBA=45°,∠CBA=105°.(参考数据: