题目内容
8.已知长方形的周长为180厘米,两邻边长分别为x厘米、y厘米,且x3+x2y-4xy2-4y3=0,求长方形的面积.分析 把x3+x2y-4xy2-4y3=0化简成(x+y)(x+2y)(x-2y),可得x=2y,由题意可得x+y=90,解方程组$\left\{\begin{array}{l}{x=2y}\\{x+y=90}\end{array}\right.$即可.
解答 解:∵x3+x2y-4xy2-4y3=0,
∴x2(x+y)-4y2(x+y)=0,
∵(x+y)(x+2y)(x-2y)=0,
∵x+y>0,x+2y>0,
∴x=2y.
又由题意可得x+y=90,
解方程组$\left\{\begin{array}{l}{x=2y}\\{x+y=90}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=60}\\{y=30}\end{array}\right.$.
∴长方形的面积=60×30=1800(平方厘米).
点评 本题是因式分解在学科内的综合运用,主要考查了分组分解法,提取公因式法和运用平方差公式法.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
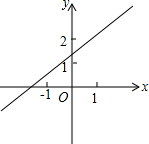 直线l:y=(m-3)x+n(m,n为常数)如图所示,化简|m-n+3|+$\sqrt{{n}^{2}-4n+4}$-|m-1|.
直线l:y=(m-3)x+n(m,n为常数)如图所示,化简|m-n+3|+$\sqrt{{n}^{2}-4n+4}$-|m-1|.