题目内容
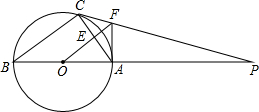 如图,△ABC内接⊙O,AB是直径,⊙O的切线PC交BA的延长线于点P,OF∥BC交AC于点E,交PC于点F,若AC=24,AF=15,求圆的半径.
如图,△ABC内接⊙O,AB是直径,⊙O的切线PC交BA的延长线于点P,OF∥BC交AC于点E,交PC于点F,若AC=24,AF=15,求圆的半径.考点:切线的性质
专题:
分析:如图,作辅助线,构造全等三角形;证明△OCF≌△QAF,进而证明△AOF为直角三角形;运用垂径定理及射影定理即可解决问题.
解答: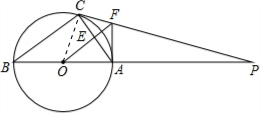 解:如图,连接OC;
解:如图,连接OC;
∵AB是⊙O的直径,
∴AC⊥BC;
又∵OF∥BC,
∴OF⊥AC,
∴AE=CE=12(垂径定理),
∴FC=FA;
在△OCF与△OAF中,
,
∴△OCF≌△OAF(SSS),
∴∠OAF=∠OCF,
∵PC为⊙O的切线,
∴OC⊥CF,
∴∠OAF=∠OCF=90°,
由勾股定理得:
EF2=FA2-AE2=152-122,
∴EF=9;
由射影定理得:AE2=OE•EF,
∴OE=
=16
又∵OA2=OE•OF=16×(16+9),
∴OA=20,
即⊙O的半径为20.
 解:如图,连接OC;
解:如图,连接OC;∵AB是⊙O的直径,
∴AC⊥BC;
又∵OF∥BC,
∴OF⊥AC,
∴AE=CE=12(垂径定理),
∴FC=FA;
在△OCF与△OAF中,
|
∴△OCF≌△OAF(SSS),
∴∠OAF=∠OCF,
∵PC为⊙O的切线,
∴OC⊥CF,
∴∠OAF=∠OCF=90°,
由勾股定理得:
EF2=FA2-AE2=152-122,
∴EF=9;
由射影定理得:AE2=OE•EF,
∴OE=
| 122 |
| 9 |
又∵OA2=OE•OF=16×(16+9),
∴OA=20,
即⊙O的半径为20.
点评:该命题以圆为载体,以考查切线的性质、勾股定理、射影定理等几何知识点为核心构造而成;解题的关键是灵活运用有关知识点来分析、判断、计算或推理.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
下列各数是无理数的是( )
| A、0 | ||||
| B、π | ||||
| C、3.14 | ||||
D、
|
 如图,AB是⊙O的直径,弦CD⊥AB,∠ACD=30°,CD=6,则由
如图,AB是⊙O的直径,弦CD⊥AB,∠ACD=30°,CD=6,则由 |
| AD |
A、
| ||
| B、π | ||
| C、2π | ||
| D、4π |

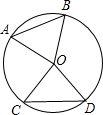 如图,在⊙O中,AB、CD是弦,根据条件填空.
如图,在⊙O中,AB、CD是弦,根据条件填空. 如图,D、E、F、B在一条直线上,AB=CD,∠B=∠D,BF=DE.
如图,D、E、F、B在一条直线上,AB=CD,∠B=∠D,BF=DE.