题目内容
某位篮球运动员在同样的条件下进行投篮练习,结果如下表:
(1)将上表补充完整;
(2)这位运动员投篮一次,进球的概率约是多少?
(3)若这位运动员投篮10次,必定会投进8次吗?为什么?
| 投篮次数(n) | 8 | 10 | 15 | 20 | 30 | 40 | 50 | ||
| 进球次数(m) | 6 | 8 | 12 | 17 | 25 | 32 | 38 | ||
进球频率(
|
(2)这位运动员投篮一次,进球的概率约是多少?
(3)若这位运动员投篮10次,必定会投进8次吗?为什么?
考点:利用频率估计概率
专题:计算题
分析:(1)分别计算,结果保留两个小数即可;
(2)根据利用概率估计频率,所计算的频率都在0.8左右波动,所以可估计进球的概率约是0.8;
(3)根据概率的意义进行回答.
(2)根据利用概率估计频率,所计算的频率都在0.8左右波动,所以可估计进球的概率约是0.8;
(3)根据概率的意义进行回答.
解答:解:(1)答案为:0.75;0.8;0.8;0.85;0.83;0.8;0.76;
(2)这位运动员投篮一次,进球的概率约是0.8;
(3)若这位运动员投篮10次,不一定会投进8次.因为进球的概率是0.8是通过大量重复实验得到的,而投篮10次是随机的,所以不一定会投进8次,也可能都不进,也可能都进.
(2)这位运动员投篮一次,进球的概率约是0.8;
(3)若这位运动员投篮10次,不一定会投进8次.因为进球的概率是0.8是通过大量重复实验得到的,而投篮10次是随机的,所以不一定会投进8次,也可能都不进,也可能都进.
点评:本题考查了利用概率估计频率:当实验的所有可能结果不是有限个或结果个数很多,或各种可能结果发生的可能性不相等时,一般通过统计频率来估计概率.

练习册系列答案
相关题目
一款手机连续两次降价,由原来的1299元降到688元.设平均每次降价的百分率为x,则列方程为( )
| A、688(1+x)2=1299 |
| B、1299(1+x)2=688 |
| C、688(1-x)2=1299 |
| D、1299(1-x)2=688 |
在实数
,-
,-3.14,0,2π,
中,无理数有( )
| 1 |
| 3 |
| 3 |
| 3 | -27 |
| A、1个 | B、2个 | C、3个 | D、4个 |
 如图所示,直线y=x+a-2与双曲线y=
如图所示,直线y=x+a-2与双曲线y= 已知CD是Rt△ABC斜边上的高线,且AB=10,若sin∠ACD=
已知CD是Rt△ABC斜边上的高线,且AB=10,若sin∠ACD= 如图,在纸片△ABC中,AC=6,∠A=30°,∠C=90°,将∠A沿DE折叠,使点A与点B重合,则折痕DE的长为
如图,在纸片△ABC中,AC=6,∠A=30°,∠C=90°,将∠A沿DE折叠,使点A与点B重合,则折痕DE的长为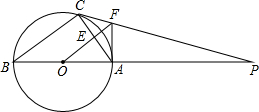 如图,△ABC内接⊙O,AB是直径,⊙O的切线PC交BA的延长线于点P,OF∥BC交AC于点E,交PC于点F,若AC=24,AF=15,求圆的半径.
如图,△ABC内接⊙O,AB是直径,⊙O的切线PC交BA的延长线于点P,OF∥BC交AC于点E,交PC于点F,若AC=24,AF=15,求圆的半径.