题目内容
10. 如图,已知△ABC,直线PQ垂直平分AC,与边AB交于点E,连接CE,过点C作CF∥BA交PQ于点F,连接AF.
如图,已知△ABC,直线PQ垂直平分AC,与边AB交于点E,连接CE,过点C作CF∥BA交PQ于点F,连接AF.(1)求证:△AED≌△CFD;
(2)求证:四边形AECF是菱形.
(3)若ED=6,AE=10,则菱形AECF的面积是多少?
分析 (1)由PQ为线段AC的垂直平分线得到AE=CE,AD=CD,然后根据CF∥AB得到∠EAC=∠FCA,∠CFD=∠AED,利用ASA证得两三角形全等即可;
(2)根据全等得到AE=CF,然后根据EF为线段AC的垂直平分线,得到EC=EA,FC=FA,从而得到EC=EA=FC=FA,利用四边相等的四边形是菱形判定四边形AECF为菱形;
(3)由菱形的性质和勾股定理求出AD,得出AC的长,由菱形的面积公式即可得出结果.
解答 (1)证明:∵PQ为线段AC的垂直平分线,
,∴AE=CE,AD=CD,
∵CF∥AB,
∴∠EAC=∠FCA,∠CFD=∠AED,
在△AED与△CFD中,$\left\{\begin{array}{l}{EAC=∠FCA}&{\;}\\{∠CFD=∠AED}&{\;}\\{AD=CD}&{\;}\end{array}\right.$
∴△AED≌△CFD(AAS);
(2)证明:∵△AED≌△CFD,
∴AE=CF,
∵EF为线段AC的垂直平分线,
∴EC=EA,FC=FA,
∴EC=EA=FC=FA,
∴四边形AECF为菱形;
(3)解:∵四边形AECF是菱形,
∴AC⊥EF,
∵ED=6,AE=10,
∴EF=2ED=12,AD=$\sqrt{1{0}^{2}-{6}^{2}}$=8.
∴AC=2AD=16,
∴菱形AECF的面积=$\frac{1}{2}$AC•EF=$\frac{1}{2}$×16×12=96.
点评 本题考查了菱形的判定与性质、全等的判定与性质、盖棺定论、基本作图、线段垂直平分线的性质,解题的关键是了解通过作图能得到直线的垂直平分线.

练习册系列答案
相关题目
18.现有A、B两种商品,买3件A商品和2件B商品用了160元,买2件A商品和3件B商品用了190元.如果准备购买A、B两种商品共10件,下列方案中费用最低的为( )
| A. | A商品7件和B商品3件 | B. | A商品6件和B商品4件 | ||
| C. | A商品5件和B商品5件 | D. | A商品4件和B商品6件 |
15. 如图,在平面直角坐标系中,△ABC绕某一点P旋转一定的角度得到△A′B′C′,根据图形变换前后的关系可得点P的坐标为( )
如图,在平面直角坐标系中,△ABC绕某一点P旋转一定的角度得到△A′B′C′,根据图形变换前后的关系可得点P的坐标为( )
 如图,在平面直角坐标系中,△ABC绕某一点P旋转一定的角度得到△A′B′C′,根据图形变换前后的关系可得点P的坐标为( )
如图,在平面直角坐标系中,△ABC绕某一点P旋转一定的角度得到△A′B′C′,根据图形变换前后的关系可得点P的坐标为( )| A. | (0,1) | B. | (1,-1) | C. | (0,-1) | D. | (1,0) |
2. 如图,直线AB,CD相交于点O,OE⊥CD,∠BOE=58°,则∠AOC等于( )
如图,直线AB,CD相交于点O,OE⊥CD,∠BOE=58°,则∠AOC等于( )
 如图,直线AB,CD相交于点O,OE⊥CD,∠BOE=58°,则∠AOC等于( )
如图,直线AB,CD相交于点O,OE⊥CD,∠BOE=58°,则∠AOC等于( )| A. | 58° | B. | 42° | C. | 32° | D. | 22° |
19.若a>b,则下列式子正确的是( )
| A. | -3a>-3b | B. | a-3>b-3 | C. | $\frac{3-a}{2}$>$\frac{3-b}{2}$ | D. | a+3b<4b |
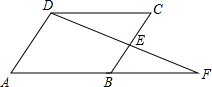 如图,在菱形ABCD中,点E是BC的中点,连接DE并延长与AB的延长线交于点F.
如图,在菱形ABCD中,点E是BC的中点,连接DE并延长与AB的延长线交于点F.