题目内容
甲、乙两个机器人分别从相距70m的A、B两个位置同时相向运动.甲第1分钟走2m,以后每分钟比前1分钟多走1m,乙每分钟走5m.
(I)甲、乙开始运动后多少分钟第一次同时到达同一位置?
(II)如果甲、乙到达A或B后立即折返,甲继续每分钟比前1分钟多走1m,乙继续按照每分钟5m的速度行走,那么开始运动后多少分钟第二次同时到达同一位置?
(I)甲、乙开始运动后多少分钟第一次同时到达同一位置?
(II)如果甲、乙到达A或B后立即折返,甲继续每分钟比前1分钟多走1m,乙继续按照每分钟5m的速度行走,那么开始运动后多少分钟第二次同时到达同一位置?
考点:应用类问题
专题:
分析:(1)根据题意先设n分钟后第1次相遇,利用数列求和知识得到关于n的方程,解此方程即可得甲、乙开始运动后几分钟相遇;
(2)先设n分钟后第2次相遇,依路程关系得到一个关于n的方程,解方程即得第2次相遇是在开始后多少分钟.
(2)先设n分钟后第2次相遇,依路程关系得到一个关于n的方程,解方程即得第2次相遇是在开始后多少分钟.
解答:解:(1)设n分钟后第1次相遇,依题意,有
+5n=70,
整理得n2+13n-140=0,
解得n=7,n=-20(舍)
第1次相遇是在开始后7分钟.
(2)设n分钟后第2次相遇,依题意,有
+5n=3×70,
整理得n2+13n-420=0,
解得n=15,n=-28(舍)
故第2次相遇是在开始后15分钟.
| n(n+3) |
| 2 |
整理得n2+13n-140=0,
解得n=7,n=-20(舍)
第1次相遇是在开始后7分钟.
(2)设n分钟后第2次相遇,依题意,有
| n(n+3) |
| 2 |
整理得n2+13n-420=0,
解得n=15,n=-28(舍)
故第2次相遇是在开始后15分钟.
点评:本小题主要考查应用类问题中函数模型的选择与应用,数列求和等基础知识,考查运算求解能力.属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

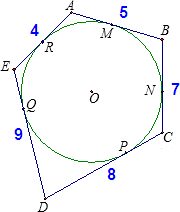 如图,已知圆O内切于五边形ABCDE,切点分别是M、N、P、Q、R,且AB=5,BC=7,CD=8,DE=9,EA=4,则
如图,已知圆O内切于五边形ABCDE,切点分别是M、N、P、Q、R,且AB=5,BC=7,CD=8,DE=9,EA=4,则 如图,半径为2的⊙O与正方形ABCD相切于点P、Q,弦MN=2,且MN在正方形的对角线BD上,则正方形的边长为
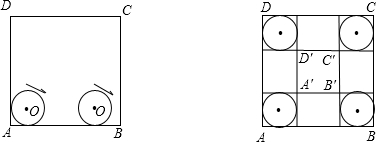
如图,半径为2的⊙O与正方形ABCD相切于点P、Q,弦MN=2,且MN在正方形的对角线BD上,则正方形的边长为